已知矩阵M＝
有特征值λ1＝4及对应的一个特征向量e1＝
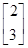.求：
(1)矩阵M；
(2)曲线5x2＋8xy＋4y2＝1在M的作用下的新曲线方程．
已知数列
的前n项和为
，且
．
（1）求数列的通项；
（2）若数列
中，
，点P（
，
）在直线
上，记的前n项和为
，当
时，试比较
与
的大小．
选修4—5；不等式选讲
已知a,b,c,d都是实数，且a2+b2=1,c2+d2=1,求证：|ac+bd|≤1.
选修4－4：坐标系与参数方程
求点P（2，
）到直线
的距离。
选修4－1：几何证明选讲
△ABC内接于⊙O，AB=AC，直线MN切⊙O于C，弦BD∥MN，AC、BD交于点E
（1）求证：△ABE≌△ACD
（2）AB=6，BC=4，求AE
已知圆
为圆上一动点，点
在
上，点
在
上，且满足
的轨迹为曲线
．
（1）求曲线的方程；
（2）若直线
与（1）中所求点的轨迹交于不同两点
是坐
标原点，且
，求△
的面积的取值范围.