已知曲线C1的参数方程为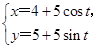 (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sin θ.
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sin θ.
(1)把C1的参数方程化为极坐标方程;
(2)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π).
已知函数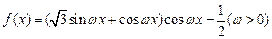 最小正周期为
最小正周期为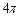
(1)求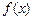 的单调递增区间
的单调递增区间
(2)在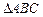 中,角
中,角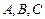 的对边分别是
的对边分别是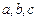 ,满足
,满足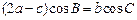 ,求函数
,求函数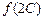 的取值范围
的取值范围
在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PA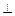 底面ABCD,点M是棱PC的中点,AM
底面ABCD,点M是棱PC的中点,AM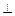 PBD.
PBD.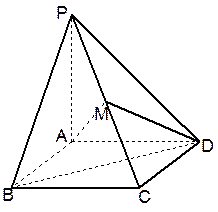
(1)求PA的长
(2)证明PB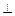 平面AMD
平面AMD
(3)求棱PC与平面AMD所成角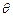 的余弦值.
的余弦值.
设函数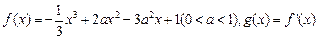 .
.
(1)求函数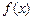 的极大值
的极大值
(2)若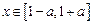 时,恒有
时,恒有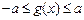 成立,试确定实数
成立,试确定实数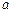 的取值范围.
的取值范围.
在平面直角坐标系中,已知点 ,向量
,向量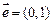 ,点B为直线
,点B为直线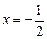 上的动点,点C满足
上的动点,点C满足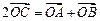 ,点M满足
,点M满足 .
.
(1)试求动点M的轨迹E的方程;
(2)设点P是轨迹E上的动点,点R、N在 轴上,圆
轴上,圆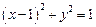 内切于
内切于 ,求
,求 的面积的最小值.
的面积的最小值.
把定义域为R的6个函数:
 ,分别写在6张小卡片上,放入盒中.
,分别写在6张小卡片上,放入盒中.
(1)现从盒子中任取2张卡片,将卡片上的函数相加得到一个新函数,求所得函数是偶函数的概率;
(2)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有奇函数卡片则停止抽取,否则继续进行,求抽取次数 的分布列和数学期望.
的分布列和数学期望.