在平面直角坐标系中,已知点 ,向量
,向量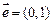 ,点B为直线
,点B为直线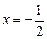 上的动点,点C满足
上的动点,点C满足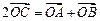 ,点M满足
,点M满足 .
.
(1)试求动点M的轨迹E的方程;
(2)设点P是轨迹E上的动点,点R、N在 轴上,圆
轴上,圆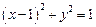 内切于
内切于 ,求
,求 的面积的最小值.
的面积的最小值.
)(如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0, 1),此时圆上一点P的位置在(0, 0),圆在x轴上沿正向滚动。当圆滚动到圆心位于(2, 1)时,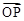 的坐标为______.
的坐标为______.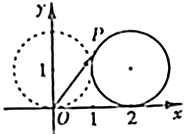
(2)在矩形ABCD中,边AB、AD的长分别为2、1,若M、N分别是边BC、CD上的点,且满足 ,则
,则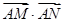 的取值范围是________.
的取值范围是________.
已知定义在实数集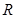 上的奇函数
上的奇函数 (
(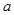 、
、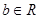 )过已知点
)过已知点 .
.
(Ⅰ)求函数的解析式;
(Ⅱ)试证明函数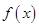 在区间
在区间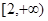 是增函数;若函数
是增函数;若函数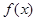 在区间
在区间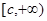 (其中
(其中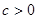 )也是增函数,求
)也是增函数,求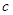 的最小值;
的最小值;
(Ⅲ)试讨论这个函数的单调性,并求它的最大值、最小值,在给出的坐标系(见答题卡)中画出能体现主要特征的图简;
(Ⅳ)求不等式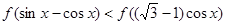 的解集.
的解集.
已知向量 ,设函数
,设函数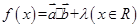 的图象关于直线
的图象关于直线 =π对称,其中
=π对称,其中 为常数,且
为常数,且 .
.
(Ⅰ)求函数 的最小正周期;
的最小正周期;
(Ⅱ)若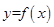 的图象经过点
的图象经过点 ,求函数
,求函数 在区间
在区间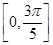 上的取值范围.
上的取值范围.
在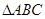 中,已知
中,已知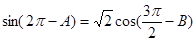 ,
,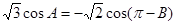 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求三个内角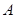 、
、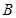 、
、 的值.
的值.
已知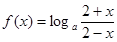 (
(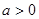 且
且 ).
).
(Ⅰ)求 的定义域;
的定义域;
(Ⅱ)求使 的
的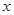 取值范围.
取值范围.