已知椭圆C： 过点M（2，3）,点A为其左顶点，且AM的斜率为 ，
（1）求C的方程；
（2）点N为椭圆上任意一点，求△AMN的面积的最大值.
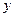
（1）令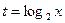
,求y关于t的函数关系式,t的范围.
（2）求该函数的值域.
甲、乙、丙三人在该市乘坐出租汽车收费情况如下表所示：
| 序号 |
里程(km) |
收费额(元) |
| 甲 |
3 |
8 |
| 乙 |
5 |
11 |
| 丙 |
8 |
20 |
试将该市出租汽车收费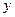
(元)表示为里程
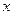(km)的函数
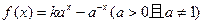
（1）求常数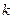
的值；
（2）若
，
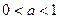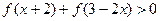，求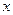
的取值范围；
（3）若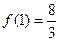
，且函数
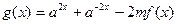在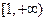
上的最小值为
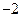，求
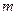的值
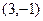
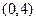
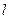
（1）若AB=8，求直线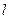的方程；
（2）当直线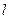的斜率为
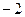时，在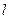上求一点P，使P到圆C的切线长等于PS；
（3）设AB的中点为N，试在平面上找一定点M，使MN的长为定值
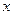
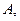
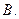
（1）当△AOB的面积达到最大值时，求四边形AOBM外接圆方程；
（2）若直线
将四边形
分割成面积相等的两部分，求△AOB的面积