已知椭圆C: 过点M(2,3),点A为其左顶点,且AM的斜率为 ,
(1)求C的方程;
(2)点N为椭圆上任意一点,求△AMN的面积的最大值.
在 中,角
中,角 所对的边分别为
所对的边分别为 ,且满足
,且满足 .
.
(1)求角 的大小;
的大小;
(2)现给出三个条件:① ;②
;② ;③
;③ .试从中选出两个可以确定
.试从中选出两个可以确定 的条件,写出你的选项,并以此为依据求出
的条件,写出你的选项,并以此为依据求出 的面积(只需写出一个选定方案即可).
的面积(只需写出一个选定方案即可).
已知 是等差数列,其前
是等差数列,其前 项和为
项和为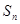 ;
; 是等比数列,且
是等比数列,且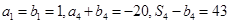 .
.
(1)求数列 与
与 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和 .
.
如图,要计算东湖岸边两景点 与
与 的距离,由于地形的限制,需要在岸上选取
的距离,由于地形的限制,需要在岸上选取 和
和 两点,现测得
两点,现测得 ,
, ,
, ,
, ,
, ,试求两景点
,试求两景点 与
与 的距离.
的距离.
已知不等式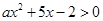 的解集是
的解集是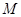 .
.
(1)若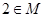 ,求
,求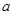 的取值范围;
的取值范围;
(2)若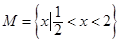 ,求不等式
,求不等式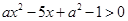 的解集.
的解集.
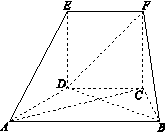
在如图所示的几何体中,面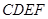 为正方形,面
为正方形,面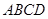 为等腰梯形,
为等腰梯形,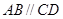 ,
,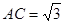 ,
, ,
, .
.
(1)求证: ;
;
(2)求三棱锥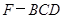 的体积;
的体积;
(3)线段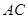 上是否存在点
上是否存在点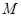 ,使
,使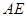 //平面
//平面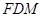 ?证明你的结论.
?证明你的结论.