已知 是椭圆 的两个焦点,P为C上一点,O为坐标原点.
(1)若 为等边三角形,求C的离心率;
(2)如果存在点P,使得 ,且 的面积等于16,求b的值和a的取值范围.
已知函数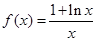 .
.
(1)若函数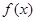 在区间
在区间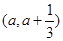
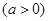 上存在极值点,求实数a的取值范围;
上存在极值点,求实数a的取值范围;
(2)如果当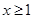 时,不等式
时,不等式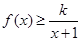 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围;
如图1,直角梯形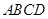 中,
中,
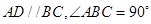 ,
,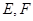 分别为边
分别为边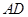 和
和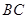 上的点,且
上的点,且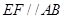 ,
,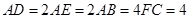 .将四边形
.将四边形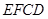 沿
沿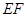 折起成如图2的位置,使
折起成如图2的位置,使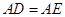 .
.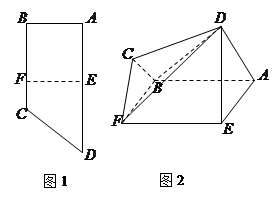
(1)求证: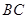
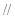 平面
平面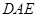 ;
;
(2)求四棱锥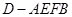 的体积.
的体积.
某停车场临时停车按时段收费,收费标准为:每辆汽车一次停车不超过1小时收费6元,超过1小时的部分每小时收费8元(不足1小时按1小时计算).现有甲、乙两人在该场地停车,两人停车都不超过4小时.
(Ⅰ)若甲停车1小时以上且不超过2小时的概率为 ,停车付费多于14元的概率为
,停车付费多于14元的概率为 ,求甲停车付费6元的概率;
,求甲停车付费6元的概率;
(Ⅱ)若甲、乙两人每人停车的时长在每个时段的可能性相同,求甲乙二人停车付费之和为28元的概率.
已知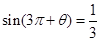 ,求
,求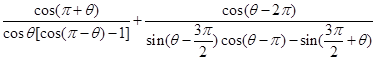 的值
的值
如图:内接于⊙O的△ABC的两条高线AD、BE相交于点H,过圆心O作OF⊥BC于 F,连接AF交OH于点G,并延长CO交圆于点I.
(1) 若 ,试求
,试求 的值;
的值;
(2)若 ,试求
,试求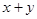 的值;
的值;
(3)若O为原点,点B的坐标为(-4,-3),点C的坐标为C(4,-3),试求点G的轨迹方程.