如图,直四棱柱 ABCD-A 1 B 1 C 1 D 1的底面是菱形, AA 1=4, AB=2,∠ BAD=60°, E, M, N分别是 BC, BB 1, A 1 D的中点.

(1)证明: MN∥平面 C 1 DE;
(2)求点 C到平面 C 1 DE的距离.
已知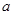 是实数,函数
是实数,函数 .
.
(1)若 ,求
,求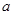 的值及曲线
的值及曲线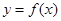 在点
在点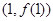 处的切线方程.
处的切线方程.
(2)求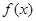 在
在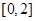 上的最大值.
上的最大值.
已知圆G: 经过椭圆
经过椭圆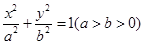 的右焦点F及上顶点B,过椭圆外一点(m,0)(
的右焦点F及上顶点B,过椭圆外一点(m,0)( )倾斜角为
)倾斜角为 的直线L交椭圆与C、D两点.
的直线L交椭圆与C、D两点.
(1)求椭圆的方程;
(2)若右焦点F在以线段CD为直径的圆E的内部,求m的取值范围.
已知侧棱垂直于底面的四棱柱,ABCD-A1B1C1D1的底面是菱形,且AD="A" A1,
点F为棱BB1的中点,点M为线段AC1的中点.
(1)求证: MF∥平面ABCD
(2)求证:平面AFC1⊥平面ACC1A1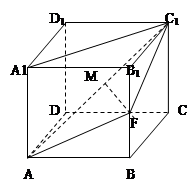
某县为增强市民的环境保护意识,面向全县征召义务宣传志愿者,先从符合条件的志愿者中随机抽取100名按年龄分组:第1组 第2组
第2组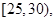 第3组
第3组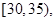 第4组
第4组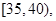 第5组
第5组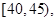 得到的频率分布直方图如图所示,
得到的频率分布直方图如图所示,
(1)分别求第3,4,5组的频率。
(2)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参与广场的宣传活动,应从第3,4,5组各抽取多少名志愿者.
(3)在(2)的条件下,该县决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.
设△ABC的内角A、B、C所对的边分别为a、b、c,且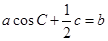 .
.
(1)求角A的大小; (2)若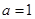 ,求△ABC的周长L的取值范围.
,求△ABC的周长L的取值范围.