已知角α的顶点与原点O重合,始边与x轴的非负半轴重合,它的终边过点P( ).
(Ⅰ)求sin(α+π)的值;
(Ⅱ)若角β满足sin(α+β)= ,求cosβ的值.
(本小题满分10分)选修4—4:坐标系与参数方程
已知曲线C的极坐标方程是ρ=4cosθ,以极点为平面直角坐标系的原点,极轴为χ轴的正半轴,建立平
面直角坐标系,直线l的参数方程是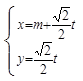 (t是参数).
(t是参数).
(Ⅰ)将曲线C的极坐标方程化为直角坐标方程,直线l的参数方程化为普通方程;
(Ⅱ)若直线l与曲线C相交于A、B两点,且|AB|= ,试求实数m的值.
,试求实数m的值.
(本小题满分10分)选修4—1:几何证明选讲
如图,AB是⊙O的直径,AC是⊙O的一条弦,∠BAC的平分线AD交⊙O于点D,DE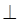 AC,且DE交AC的延长线于点E,OE交AD于点F.
AC,且DE交AC的延长线于点E,OE交AD于点F.
(Ⅰ)求证:DE是⊙O的切线;
(Ⅱ)若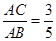 ,求
,求 的值.
的值.
(本小题满分12分)已知函数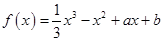 的图象在点P
的图象在点P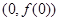 处的切线方程为
处的切线方程为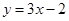 .
.
(Ⅰ)求实数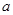 ,
, 的值;
的值;
(Ⅱ)设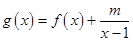 是[2,+
是[2,+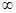 )上的增函数,求实数m的最大值.
)上的增函数,求实数m的最大值.
(本小题满分12分)已知椭圆

 过点M(0,2),离心率
过点M(0,2),离心率 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)设过定点N(2,0)的直线l与椭圆相交于A、B两点,且∠AOB为锐角(其中O为坐标原点),求直
线l斜率的取值范围.
(本小题满分12分)从某学校 的800名男生中随机抽取50名测量身高,被测学生身高全部介
于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165)……
第八组[190,195].如图是按上述分组方法得到的频率分布直方图的一部份,已知第一组与第八组人数
相同,第六组的人数为4人.
(Ⅰ)求第七组的频率;
(Ⅱ)估计该校的800名男生的身高的中位数以及身高在180cm以上(含180cm)的人数;
(Ⅲ)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为 ,
,
事件 ,事件
,事件 ,求概率
,求概率 .
.