如图,边长为2的正方形 所在的平面与半圆弧 所在平面垂直, 是 上异于 , 的点.
(1)证明:平面 平面 ;
(2)当三棱锥 体积最大时,求面 与面 所成二面角的正弦值.

已知数列 为正常数,且
为正常数,且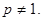
(1)求数列 的通项公式;
的通项公式;
(2)设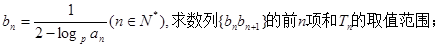
(3)是否存在正整数M,使得 恒成立?若存在,求出相应的M的最小值;若不存在,请说明理由。
恒成立?若存在,求出相应的M的最小值;若不存在,请说明理由。
(1)已知当 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围
(2)解关于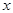 的不等式
的不等式 .
.
如图所示,要用栏杆围成一个面积为50平方米的长方形花园,其中有一面靠墙不需要栏杆,其中正面栏杆造价每米200元,两个侧面栏杆每米造价50元,设正面栏杆长度为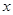 米.
米.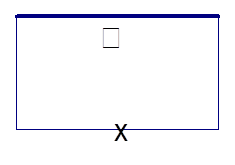
(1)将总造价y表示为关于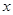 的函数;
的函数;
(2)问花园如何设计,总造价最少?并求最小值.
已知等差数列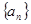 的第二项为8,前10项和为185。
的第二项为8,前10项和为185。
(1)求数列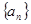 的通项公式;
的通项公式;
(2)若从数列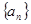 中,依次取出第2项,第4项,第8项,……,第
中,依次取出第2项,第4项,第8项,……,第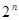 项,……按原来顺序组成一个新
项,……按原来顺序组成一个新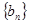 数列,试求数列
数列,试求数列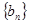 的通项公式和前n项的和
的通项公式和前n项的和
已知△ABC中,各点的坐标分别为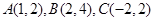 ,求:
,求:
(1)BC边上的中线AD的长度和方程;
(2)△ABC的面积.