已知抛物线C： =2px经过点 （1，2）．过点Q（0，1）的直线l与抛物线C有两个不同的交点A，B，且直线PA交y轴于M，直线PB交y轴于N．
（Ⅰ）求直线l的斜率的取值范围；
（Ⅱ）设O为原点， ， ，求证： 为定值．
已知椭圆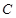
:
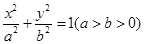的一个顶点为
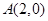，离心率为
．直线
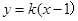与椭圆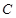交于不同的两点M，N．
（Ⅰ）求椭圆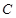的方程；
（Ⅱ）当△AMN得面积为
时，求
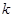的值．
等比数列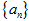
的各项均为正数，且
（1）求数列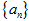的通项公式；
（2）设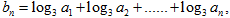
求数列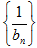
的前n项和．
如图，在直三棱柱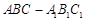
中，
，
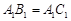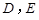分别是棱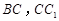
上的点（点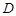
不同于点
），且
为
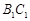的中点．
求证：（1）平面
平面
；
（2）直线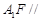
平面
．
设函数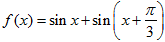
．
（1）求f（x）的最小值，并求使f（x）取得最小值的x的集合；
（2）在△ABC中，设角A，B的对边分别为a，b，若B=2A，且
，求角C的大小．
已知p：方程2x2-2mx＋1=0有两个不相等的负实根；q：存在x∈R，
x2＋mx＋1<0．若p或q为真，p且q为假，求实数m的取值范围．