(Ⅰ)
(II)
改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校所有的1000名学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
|
支付金额 支付方式 |
不大于 元 |
大于 元 |
|
仅使用A |
27人 |
3人 |
|
仅使用B |
24人 |
1人 |
(Ⅰ)估计该校学生中上个月A,B两种支付方式都使用的人数;
(Ⅱ)从样本仅使用B的学生中随机抽取1人,求该学生上个月支付金额大于 元的概率;
(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用B的学生中随机抽查1人,发现他本月的支付金额大于 元.结合(Ⅱ)的结果,能否认为样本仅使用B的学生中本月支付金额大于 元的人数有变化?说明理由.
设 是等差数列, ,且 , , 成等比数列.
(Ⅰ)求 的通项公式;
(Ⅱ)记 的前 n项和为 ,求 的最小值.
在 中, , , .
(Ⅰ)求 b, c的值;
(Ⅱ)求 的值.
在平面直角坐标系 中,椭圆 的离心率为 ,焦距为2.
(Ⅰ)求椭圆E的方程.
(Ⅱ)如图,该直线 交椭圆E于A,B两点,C是椭圆E上的一点,直线OC的斜率为 , 且看 ,M是线段OC延长线上一点,且 ,⊙M的半径为 ,OS,OT是⊙M的两条切线,切点分别为S,T,求 的最大值,并求取得最大值时直线l的斜率.
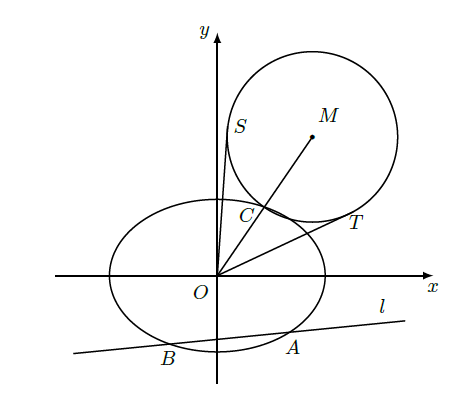
已知函数 , ,其中 是自然对数的底数.
(Ⅰ)求曲线 在点 处的切线方程;
(Ⅱ)令 ,讨论 的单调性并判断有无极值,有极值时求出极值.