已知曲线 与直线 交于两点 和 ,且 .记曲线 在点 和点 之间那一段 与线段 所围成的平面区域(含边界)为 .设点 是 上的任一点,且点 与点 和点 均不重合.
(1)若点 是线段 的中点,试求线段 的中点 的轨迹方程;
(2)若曲线 与点 有公共点,试求 的最小值.
设△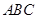 的内角
的内角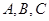 所对边的长分别是
所对边的长分别是 ,且
,且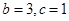 ,△
,△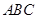 的面积为
的面积为 ,求
,求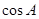 与
与 的值.
的值.
已知 .
.
(1)化简 ;
;
(2)若 是第三象限角,且
是第三象限角,且 ,求
,求 的值.
的值.
已知直线的极坐标方程为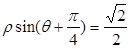 ,圆M的参数方程为
,圆M的参数方程为 。求:(1)将直线的极坐标方程化为直角坐标方程;
。求:(1)将直线的极坐标方程化为直角坐标方程;
(2)求圆M上的点到直线的距离的最小值.
(本小题满分10分)某班主任对班级22名学生进行了作业量多少的调查,数据如下表:在喜欢玩电脑游戏的12中,有10人认为作业多,2人认为作业不多;在不喜欢玩电脑游戏的10人中,有3人认为作业多,7人认为作业不多.求:
(1)根据以上数据建立一个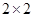 列联表;
列联表;
(2)试问喜欢电脑游戏与认为作业多少是否有关系?
在平面直角坐标系 中,以
中,以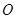 为极点,
为极点,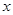 轴非负半轴为极轴建立坐标系,已知曲线
轴非负半轴为极轴建立坐标系,已知曲线 的极坐标方程为
的极坐标方程为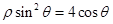 ,直线
,直线 的参数方程为:
的参数方程为:  (
(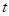 为参数),两曲线相交于
为参数),两曲线相交于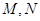 两点. 求:
两点. 求:
(1)写出曲线 的直角坐标方程和直线
的直角坐标方程和直线 的普通方程;
的普通方程;
(2)若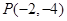 求
求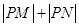 的值.
的值.