在平面直角坐标系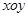 中,以
中,以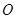 为极点,
为极点,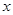 轴非负半轴为极轴建立坐标系,已知曲线
轴非负半轴为极轴建立坐标系,已知曲线 的极坐标方程为
的极坐标方程为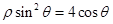 ,直线
,直线 的参数方程为:
的参数方程为:  (
(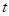 为参数),两曲线相交于
为参数),两曲线相交于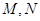 两点. 求:
两点. 求:
(1)写出曲线 的直角坐标方程和直线
的直角坐标方程和直线 的普通方程;
的普通方程;
(2)若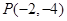 求
求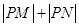 的值.
的值.
(本小题满分8分)
如图,A,B,C,D都在同一 个与水平面垂直的平面内,B,D为两岛上的两座
个与水平面垂直的平面内,B,D为两岛上的两座 灯塔的塔顶。测量船于水面A处测得B点和D点的仰角分别为
灯塔的塔顶。测量船于水面A处测得B点和D点的仰角分别为 ,
,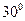 ,于水面C处测得B点和D点的仰角均为
,于水面C处测得B点和D点的仰角均为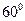 ,AC=0.1km。
,AC=0.1km。
(Ⅰ)试探究图中B,D间的距离与另外哪两点间距离会相等?
(II)求B,D间的距离。

(本小题满分6分)
在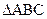 中,
中,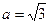 ,
, ,
, ,求边
,求边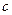 及
及
选修4—5;不等式选讲
已知f(x)=x|x-a|-2
(1)当a=1时,解不等式f(x)<|x-2|
(2)当x∈(0,1]时,f(x)< x2-1恒成立,求实数a的取值范围。
x2-1恒成立,求实数a的取值范围。
四、选考题:(本小题满分10分)
请考生在第22、23、题中任选一题做答,如果多做,则按所做的第一题记分.
22.选修4-4:坐标系与参数方程
已知圆O1和圆O2的极坐标方程分别为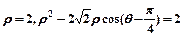
(1)把圆O1和圆O2的极坐标方程化为直角坐标方程;
(2)求经过两圆交点的直线的极坐标方程。