四、选考题:(本小题满分10分)
请考生在第22、23、题中任选一题做答,如果多做,则按所做的第一题记分.
22.选修4-4:坐标系与参数方程
已知圆O1和圆O2的极坐标方程分别为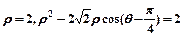
(1)把圆O1和圆O2的极坐标方程化为直角坐标方程;
(2)求经过两圆交点的直线的极坐标方程。
袋中有除颜色外完全相同的红、黄、白三种颜色的球各一个,从中每次任取1个.有放回地抽取3次,求:
(1)3个全是红球的概率;
(2)3个颜色全相同的概率;
(3)3个颜色不全相同的概率;
(4)3个颜色全不相同的概率.
从两块玉米地里各抽取10株玉米苗,分别测得它们的株高如下(单位:cm ):
甲:25 41 40 37 22 14 19 39 21 42乙:27 16 44 27 44 16 40 40 16 40
根据以上数据回答下面的问题:
(1)哪种玉米苗长得高?
(2)哪种玉米苗长得齐?
已知抛物线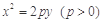 与直线
与直线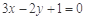 交于
交于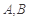 两点,
两点,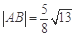 ,点
,点 在抛物线上,
在抛物线上,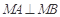 .
.
(Ⅰ) 求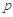 的值;
的值;
(Ⅱ) 求点 的坐标.
的坐标.
已知函数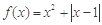 .
.
(Ⅰ)求函数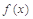 的单调递增区间;
的单调递增区间;
(Ⅱ)函数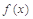 在
在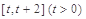 上的最大值与最小值的差为
上的最大值与最小值的差为 ,求
,求 的表达式.
的表达式.
如图,已知矩形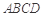 所在平面与等腰直角三角形
所在平面与等腰直角三角形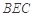 所在平面互相垂直,
所在平面互相垂直, ,
, ,
,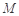 为线段
为线段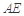 的中点.
的中点.
(Ⅰ) 证明: ;
;
(Ⅱ) 求 与平面
与平面 所成的角的余弦值.
所成的角的余弦值.