等比数列 的前n 项和为 ,已知 , , 成等差数列
(1)求 的公比 ;
(2)求
求


设函数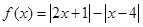 .
.
(1) 解不等式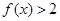 ;
;
(2) 求函数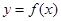 的最小值.
的最小值.
如图,已知圆中两条弦AB与CD相交于点F,E是AB延长线上一点,且DF=CF=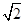 ,AF∶FB∶BE=4∶2∶1,若CE与圆相切,求线段CE的长.
,AF∶FB∶BE=4∶2∶1,若CE与圆相切,求线段CE的长.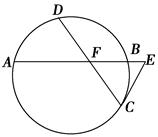
高中流行这样一句话“文科就怕数学不好,理科就怕英语不好”.下
表是一次针对高三文科学生的调查所得的数据,试问:在出错概率不超过0.01的前提下文
科学生总成绩不好与数学成绩不好有关系吗?
| 总成绩好 |
总成绩不好 |
总计 |
|
| 数学成绩好 |
20 |
10 |
30 |
| 数学成绩不好 |
5 |
15 |
20 |
| 总计 |
25 |
25 |
50 |
(P(K2≥3.841)≈0.05,P(K2≥6.635)≈0.01)
设函数
(1)求不等式 的解集;
的解集;
(2)若不等式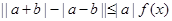 (
(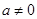 ,
,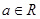 ,
,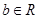 )恒成立,求实数
)恒成立,求实数 的范围.
的范围.
已知圆的极坐标方程为ρ2-4 ρ·cos
ρ·cos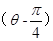 +6=0.
+6=0.
(1)将极坐标方程化为普通方程,并选择恰当的参数写出它的参数方程;
(2)若点P(x,y)在该圆上,求x+y的最大值和最小值.