为了研究一种新药的疗效,选100名患者随机分成两组,每组各 名,一组服药,另一组不服药.一段时间后,记录了两组患者的生理指标 和 的数据,并制成如图,其中“*”表示服药者,“+”表示未服药者.

(1)从服药的50名患者中随机选出一人,求此人指标 的值小于 的概率;
(2)从图中A,B,C,D四人中随机选出两人,记 为选出的两人中指标x的值大于1.7的人数,求 的分布列和数学期望 ;
(3)试判断这100名患者中服药者指标 数据的方差与未服药者指标y数据的方差的大小.(只需写出结论)
定义在 上的函数
上的函数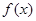 满足对任意
满足对任意 都有
都有 .
.
且 时,
时, ,
,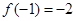
(1)求证: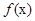 为奇函数;
为奇函数;
(2)试问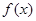 在
在 上是否有最值?若有,求出最值;若无,说明理由;
上是否有最值?若有,求出最值;若无,说明理由;
(3)若 对任意
对任意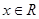 恒成立,求实数
恒成立,求实数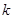 的取值范围.
的取值范围.
设 为实数,函数
为实数,函数 .
.
(1)若函数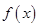 是偶函数,求实数
是偶函数,求实数 的值;
的值;
(2)若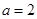 ,求函数
,求函数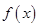 的最小值;
的最小值;
(3)对于函数 ,在定义域内给定区间
,在定义域内给定区间 ,如果存在
,如果存在 ,满足
,满足 ,则称函数
,则称函数 是区间
是区间 上的“平均值函数”,
上的“平均值函数”,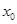 是它的一个“均值点”.如函数
是它的一个“均值点”.如函数 是
是 上的平均值函数,
上的平均值函数, 就是它的均值点.现有函数
就是它的均值点.现有函数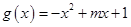 是区间
是区间 上的平均值函数,求实数
上的平均值函数,求实数 的取值范围.
的取值范围.
某村电费收取有以下两种方案供农户选择:
方案一:每户每月收管理费2元,月用电不超过30度时,每度0.5元,超过30度时,超过部分按每度0.6元收取.
方案二:不收管理费,每度0.58元.
(1)求方案一收费 元与用电量
元与用电量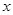 (度)间的函数关系;
(度)间的函数关系;
(2)老王家九月份按方案一交费35元,问老王家该月用电多少度?
(3)老王家月用电量在什么范围时,选择方案一比选择方案二更好?
已知函数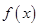 是二次函数,且满足
是二次函数,且满足 ;函数
;函数 .
.
(1)求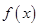 的解析式;
的解析式;
(2)若 ,且
,且 对
对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
设 ,
,
(1)若 ,求
,求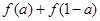 的值;
的值;
(2)求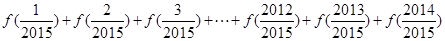 的值.
的值.