［物理--选修3-3］
（1）氧气分子在 和 温度下单位速率间隔的分子数占总分子数的百分比随气体分子速率的变化分别如图中两条曲线所示．下列说法正确的是（ ）
| A． |
图中两条曲线下面积相等 |
| B． |
图中虚线对应于氧气分子平均动能较小的情形 |
| C． |
图中实线对应于氧气分子在 时的情形 |
| D． |
图中曲线给出了任意速率区间的氧气分子数目 |
| E． |
与0℃时相比，100℃时氧气分子速率出现在 区间内的分子数占总分子数的百分比较大 |
（2）如图，容积均为V的汽缸A、B下端有细管（容积可忽略）连通，阀门 位于细管的中部，A、B的顶部各有一阀门 、 ，B中有一可自由滑动的活塞（质量、体积均可忽略）．初始时，三个阀门均打开，活塞在B的底部；关闭 、 ，通过 给汽缸充气，使A中气体的压强达到大气压p 0的3倍后关闭 ．已知室温为27℃，汽缸导热．
（i）打开 ，求稳定时活塞上方气体的体积和压强；
（ii）接着打开 ，求稳定时活塞的位置；
（iii）再缓慢加热汽缸内气体使其温度升高20℃，求此时活塞下方气体的压强．
如图所示，在光滑水平桌面上静止放置一质量为M的气缸，不计摩擦的质量为m的活塞封闭了温度为
，体积为
的一定质量的理想气体，气体与外界无热交换，大气压为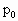
．现在又一个质量为
，速度为
的子弹水平射入活塞并留在活塞中，活塞向右推进压缩气体，设气体在推进过程中任意时刻，封闭的理想气体均处于相应的平衡状态．当气体压缩到最小体积为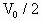
时，压强为2.5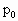．求：
(1)此时气体的温度；
(2)活塞压缩气体过程中内能的增量．
如图所示，均匀薄壁U形管，左管上端封闭，右管开口且足够长，管的横截面积为S，内装密度为ρ的液体．右管内有一质量为m的活塞搁在固定卡口上，卡口与左管上端等高，活塞与管壁间无摩擦且不漏气．温度为
时，左、右管内液面高度相等，两管内空气柱长度均为l，压强均为大气压强
．现使两边温度同时逐渐升高，求：
(1)温度升高到多少时，右管活塞开始离开卡口上升？
(2)温度升高到多少时，左管内液面下降h？
如图所示，横截面积S=10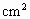
的圆筒上、下部均与大气相通，竖直固定在水平地面上，活塞A与B将一定质量的空气封闭在圆筒中部，活塞A质量
=1kg，活塞B用一轻弹簧与地面相连，弹簧劲度系数k=1000N/m，当活塞处于平衡状态时，被封闭气体长度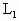
=16cm．现用一恒力F将活塞A向上拉，当两活塞重新平衡时，活塞B向上移动了3cm．已知大气压强
=1.0×
Pa，不计活塞与筒壁摩擦．求拉力F的大小及活塞A上移距离ΔL(此过程中温度保持不变)．
如图所示，一根横截面积S=1
的长管，两端开口，竖直插入水银槽中，有两个质量都是m=20g密闭活塞A、B，在管中封闭两段长都是
=10.0cm的理想气体．开始时A、B都处于静止状态，不计管壁与A、B的摩擦．现在用力F竖直向上缓慢拉动活塞A，当F=4.2N时A、B再次静止．设整个过程中，环境温度不变，g取10m/
，外界大气压强
=1.00×
Pa，水银密度
，求在此过程中：
(1)有多高的水银柱进入管内；
(2)活塞A上升的距离．
质量一定的理想气体，被截面积为S的活塞封闭在圆柱形金属气缸内，气缸竖直放在水平地面上，活塞与气缸底部之间用一轻弹簧连接，活塞所受重力为G，活塞与气缸壁无摩擦且不漏气，如图所示．当大气压强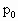
为1.0×
Pa，气体温度为27℃时，气缸内气体压强为1.2×Pa，此时弹簧恰好为原长
．现将一个物重为3G的物体轻放在活塞上，待稳定后，活塞下降了/4，温度保持不变，然后再对气体缓慢加热，使活塞上升到离气缸底部处停止加热．在整个过程中弹簧始终处于弹性限度内．
(1)试导出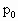S与G的关系式；
(2)试导出弹簧的劲度系数k与活塞G、弹簧原长间的关系式；
(3)求停止加热时气缸内气体的温度．