如图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.
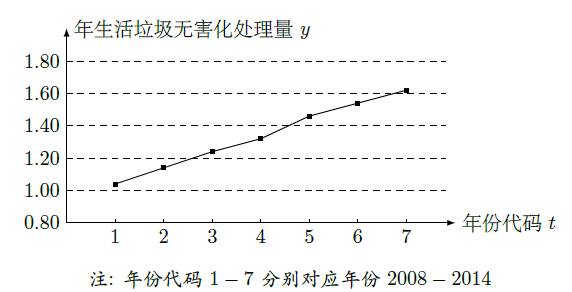
(1)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以证明;
(2)建立y关于t的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
附注:
参考数据: , , , .
参考公式: ,回归方程 中斜率和截距的最小二乘估计公式分别为:
, .
(本题13分)在数列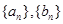 ,
,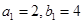 ,且
,且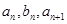 成等差数列,
成等差数列,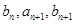 成等比数列
成等比数列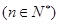
(1)求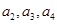 及
及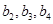 由此猜测
由此猜测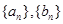 的通项公式并证明你的结论;
的通项公式并证明你的结论;
(2)证明: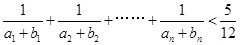 。
。
(本题12分)已知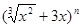 展开式各项系数和比它的二项式系数和大992。
展开式各项系数和比它的二项式系数和大992。
(1)求展开式中含有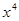 的项;
的项;
(2)求展开式中二项式系数最大的项;
(3)求展开式中系数最大的项。
(本题12分)有4个不同的小球,4个不同的盒子,现需把球全部放进盒子里,
(1)没有空盒子的方法共有多少种?
(2)可以有空盒子的方法共有多少种?
(3)恰有1个盒子不放球,共有多少种方法?(最后结果用数字作答)
(本题12分)已知复数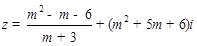
(1)m取什么值时,z是实数?
(2)m 取什么值时,z是纯虚数?
(本小题满分 分)某校高二年级某班的数学课外活动小组中有6名男生,4名女生,从中选出4人参加数学竞赛考试,用X表示其中的男生人数,求X的分布列。
分)某校高二年级某班的数学课外活动小组中有6名男生,4名女生,从中选出4人参加数学竞赛考试,用X表示其中的男生人数,求X的分布列。