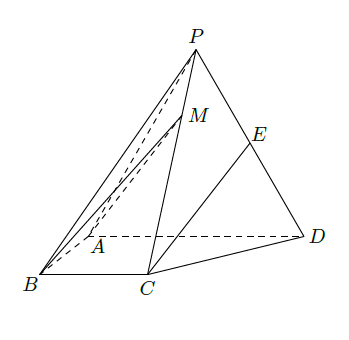
如图,四棱锥
中,侧面
为等比三角形且垂直于底面
,
是
的中点.
(1)证明:直线 平面 ;
(2)点 M在棱 PC上,且直线 BM与底面 ABCD所成锐角为 ,求二面角 的余弦值.
已知命题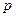 :函数
:函数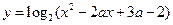 的定义域为R;命题
的定义域为R;命题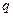 :方程
:方程 有两个不相等的负数根,若
有两个不相等的负数根,若 是假命题,求实数
是假命题,求实数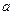 的取值范围
的取值范围
(本小题满分13分
已知函数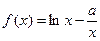 ,
,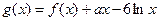 ,其中
,其中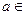 R
R
(Ⅰ)讨论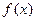 的单调性
的单调性
(Ⅱ)若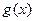 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数 的取值范围
的取值范围
(Ⅲ)设函数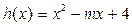 , 当
, 当 时,若
时,若 ,
,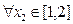 ,总有
,总有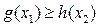 成立,求实数
成立,求实数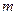 的取值范围
的取值范围
(本小题满分13分)
已知函数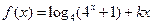
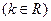 是偶函数
是偶函数
(Ⅰ)求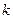 的值;
的值;
(Ⅱ)设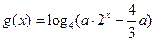 ,若函数
,若函数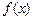 与
与 的图象有且只有一个公共点,求实数
的图象有且只有一个公共点,求实数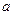 的取值范围.
的取值范围.
(本小题满分13分)某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场售价与上市时间的关系用图一的一条折线表示;西红柿的种植成本与上市时间的关系用图二的抛物线段表示.
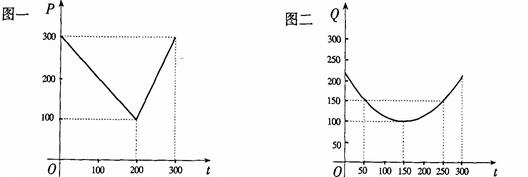 |
(Ⅰ) 写出图一表示的市场售价与时间的函数关系式P =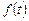 ;
;
写出图二表示的种植成本与时间的函数关系式Q =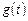 ;
;
(Ⅱ) 认定市场售价减去种植成本为纯收益,问何时上市的西红柿收益最大?
(注:市场售价和种植成本的单位:元/ kg,时间单位:天)
kg,时间单位:天)
(本小题满分12分) 一个口袋里有5个白球和3个黑球,任意取出一个,如果是黑球,则这个黑球不放回而另外放入一个白球,这样继续下去,直到取出的球是白球时结束取球。求直到取到白球所需的抽取次数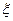 的概率分布列
的概率分布列