[选修4―4:坐标系与参数方程]
在直角坐标系 xOy中,直线
 的参数方程为
( t为参数),直线
的参数方程为
.设 l 1与 l 2的交点为 P,当 k变化时, P的轨迹为曲线 C .
的参数方程为
( t为参数),直线
的参数方程为
.设 l 1与 l 2的交点为 P,当 k变化时, P的轨迹为曲线 C .
(1)写出 C的普通方程;
(2)以坐标原点为极点, x轴正半轴为极轴建立极坐标系,设 , M为 l 3与 C的交点,求 M的极径.
已知数列 的前
的前 项和
项和 满足
满足 ,(
,( 为常数,
为常数, 且
且 ).
).
(1)求数列 的通项公式;
的通项公式;
(2)设 ,且数列
,且数列 为等比数列.
为等比数列.
①求 的值;
的值;
②若 ,求数列
,求数列 的前
的前 和
和 .
.
如图所示,正方形 所在的平面与等腰
所在的平面与等腰 所在的平面互相垂直,其中顶
所在的平面互相垂直,其中顶 ,
, ,
, 为线段
为线段 的中点.
的中点.
(1)若 是线段
是线段 上的中点,求证:
上的中点,求证: 平面
平面 ;
;
(2)若 是线段
是线段 上的一个动点,设直线
上的一个动点,设直线 与平面
与平面 所成角的大小为
所成角的大小为 ,求
,求 的最大值.
的最大值.
锐角 的内角
的内角 ,
,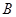 ,
,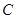 ,的对边分别为
,的对边分别为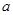 ,
,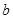 ,
,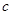 ,已知
,已知
(1)求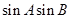 的值;
的值;
(2)若 ,
, ,求
,求 的面积.
的面积.
给定函数 和常数
和常数 ,若
,若 恒成立,则称
恒成立,则称 为函数
为函数 的一个“好数对”;若
的一个“好数对”;若 恒成立,则称
恒成立,则称 为函数
为函数 的一个“类好数对”.已知函数
的一个“类好数对”.已知函数 的定义域为
的定义域为 .
.
(1)若 是函数
是函数 的一个“好数对”,且
的一个“好数对”,且 ,求
,求 ;
;
(2)若 是函数
是函数 的一个“好数对”,且当
的一个“好数对”,且当 时,
时, ,求证:
,求证:
函数 在区间
在区间 上无零点;
上无零点;
(3)若 是函数
是函数 的一个“类好数对”,
的一个“类好数对”, ,且函数
,且函数 单调递增,比较
单调递增,比较 与
与 的大小,并说明理由.
的大小,并说明理由.
已知数列 的前
的前 项和
项和 满足
满足 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,记数列
,记数列 的前
的前 和为
和为 ,证明:
,证明: .
.