如图，在平面直角坐标系中，矩形 的边 长是方程 的根，连接 ， ，并过点 作 ，垂足为 ，动点 从点 以每秒 个单位长度的速度沿 方向匀速运动到点 为止；点 沿线段 以每秒 个单位长度的速度由点 向点 匀速运动，到点 为止，点 与点 同时出发，设运动时间为 秒
（ 1 ）线段 ______ ；
（ 2 ）连接 和 ，求 的面积 与运动时间 的函数关系式；
（ 3 ）在整个运动过程中，当 是以 为腰的等腰三角形时，直接写出点 的坐标．
如图，在平面直角坐标系xOy中，以点A（2，3）为圆心的⊙A交 x轴于点B，C，BC=8，求⊙A的半径．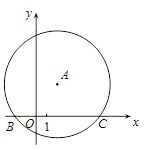
如图，△ABC中，点D在AB上，∠ACD=∠ABC，若AD=2，AB=6，求AC的长．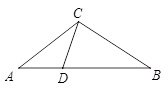
用配方法解方程：
．
如图，二次函数
的图象与x轴交于点A（﹣1，0），B（2，0），与y轴相交于点C．
（1）求二次函数的解析式；
（2）若点E是第一象限的抛物线上的一个动点，当四边形ABEC的面积最大时，求点E的坐标，并求出四边形ABEC的最大面积；
（3）若点M在抛物线上，且在y轴的右侧．⊙ M与y轴相切，切点为D．以C，D，M为顶点的三角形与△AOC相似，求点M的坐标．
如图，已知△ABC和△ADE都是等腰直角三角形，∠BAC=∠DAE=90°，AB=AC，AD=AE．连接BD交AE于M，连接CE交AB于N，BD与CE交点为F，连接AF．
（1）如图1，求证：BD⊥CE；
（2）如图1，求证：FA是∠CFD的平分线；
（3）如图2，当AC=2，∠BCE=15°时，求CF的长．