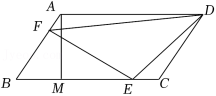
如图,平行四边形ABCD中, ,BC边上的高 ,点E为BC边上的动点(不与B、C重合,过点E作直线AB的垂线,垂足为F,连接DE、DF.
(1)求证: ;
(2)当点E为BC的中点时,求DE的长;
(3)设 ,△DEF的面积为y,求y与x之间的函数关系式,并求当x为何值时,y有最大值,最大值是多少?
解方程:4t2-(t+1)2=0.
已知抛物线y=ax2-2ax+c与y轴交于C点,与x轴交于A、B两点,点A的坐标是(-1,0),O是坐标原点,且|OC|=3|OA|
(1)求抛物线的函数表达式;
(2)直接写出直线BC的函数表达式;
(3)如图1,D为y轴的负半轴上的一点,且OD=2,以OD为边作正方形ODEF.将正方形ODEF以每秒1个单位的速度沿x轴的正方向移动,在运动过程中,设正方形ODEF与△OBC重叠部分的面积为s,运动的时间为t秒(0<t≤2).
求:①s与t之间的函数关系式;
②在运动过程中,s是否存在最大值?如果存在,直接写出这个最大值;如果不存在,请说明理由.
(4)如图2,点P(1,k)在直线BC上,点M在x轴上,点N在抛物线上,是否存在以A、M、N、P为顶点的平行四边形?若存在,请直接写出M点坐标;若不存在,请说明理由.
如图1,矩形ABCD中,AB=4,AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.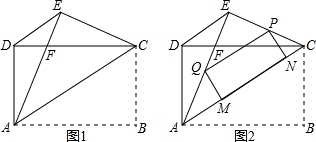
(1)求证:△DEC≌△EDA;
(2)求DF的值;
(3)如图2,若P为线段EC上一动点,过点P作△AEC的内接矩形,使其顶点Q落在线段AE上,定点M、N落在线段AC上,当线段PE的长为何值时,矩形PQMN的面积最大?并求出其最大值.
端午节期间,某品牌粽子经销商销售甲、乙两种不同味道的粽子,已知一个甲种粽子和一个乙种粽子的进价之和为10元,每个甲种粽子的利润是4元,每个乙种粽子的售价比其进价的2倍少1元,小王同学买4个甲种粽子和3个乙种粽子一共用了61元.
(1)甲、乙两种粽子的进价分别是多少元?
(2)在(1)的前提下,经销商统计发现:平均每天可售出甲种粽子200个和乙种粽子150个.如果将两种粽子的售价各提高1元,则每天将少售出50个甲种粽子和40个乙种粽子.为使每天获取的利润更多,经销商决定把两种粽子的价格都提高x元.在不考虑其他因素的条件下,当x为多少元时,才能使该经销商每天销售甲、乙两种粽子获取的利润为1190元?
解方程
(1)x2+2x-2="0"
(2)(x+2)2-10(x+2)+25=0.