某校举办“歌唱祖国”演唱比赛，十位评委对每位同学的演唱进行现场打分，对参加比赛的甲、乙、丙三位同学得分的数据进行整理、描述和分析．下面给出了部分信息．
a．甲、乙两位同学得分的折线图：
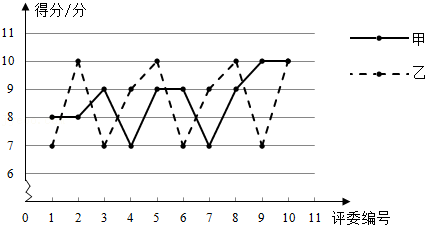
b．丙同学得分：
c．甲、乙、丙三位同学得分的平均数：
同学 |
甲 |
乙 |
丙 |
平均数 |
|
|
|
根据以上信息，回答下列问题：
（1）求表中 的值；
（2）在参加比赛的同学中，如果某同学得分的10个数据的方差越小，则认为评委对该同学演唱的评价越一致．据此推断：在甲、乙两位同学中，评委对＿＿＿＿＿的评价更一致（填“甲”或“乙”）；
（3）如果每位同学的最后得分为去掉十位评委打分中的一个最高分和一个最低分后的平均分，最后得分越高，则认为该同学表现越优秀．据此推断：在甲、乙、丙三位同学中，表现最优秀的是 ＿＿＿＿＿（填“甲”“乙”或“丙”）．
（1）解方程：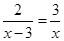 
（2）如图，AB与⊙O相切于点B，连接AO交⊙O于C，OC=BC=6，求AB.
（1）计算：
(2)已知：如图，在矩形ABCD中，点E，F分别在AB，CD边上，BE=DF，连接CE，AF．求证：AF=CE．
已知菱形ABCD的边长为1．∠ADC=60°，等边△AEF两边分别交边DC、CB于点E、F。（1）特殊发现：如图1，若点E、F分别是边DC、CB的中点．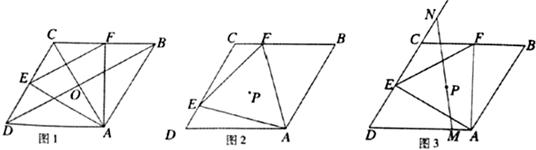
(1)求证：菱形ABCD对角线AC、BD交点O即为等边△AEF的外心；
(2)若点E、F始终分别在边DC、CB上移动．记等边△AEF的外心为点P．
①猜想验证：如图2．猜想△AEF的外心P落在哪一直线上，并加以证明；
②拓展运用：如图3，当△AEF面积最小时，过点P任作一直线分别交边DA于点M，交边DC的延长线于点N，试判断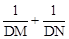
是否为定值．若是．请求出该定值；若不是．请说明理由。
已知抛物线C1的函数解析式为y＝ax2＋bx－3a（b＜0），若抛物线C1经过点（0，－3），方程ax2＋bx－3a＝0的两根为x1，x2，且
＝4．
(1)求抛物线C1的顶点坐标．
(2)已知实数x＞0，请证明x+
≥2，并说明x为何值时才会有x＋＝2．
(3)若将抛物线C1先向上平移4个单位，再向左平移1个单位后得到抛物线C2，设A（m，y1），B（n，y2）是C2上的两个不同点，且满足：∠AOB＝90°，m＞0，n＜0．请你用含m的表达式表示出△AOB的面积S，并求出S最小值及S取最小值时直线OA的函数解析式．
如图，AB为⊙O的直径，以AB为直角边作Rt△ABC，∠CAB=90°，斜边BC与⊙O交于点D，过点D作⊙O的切线DE交AC于点E，DG⊥AB于点F，交⊙O于点G．
(1)求证：E是AC的中点；(2)若AE=3，cos∠ACB=
，求弦DG的长．