受疫情影响，某初中学校进行在线教学的同时，要求学生积极参与“增强免疫力、丰富学习生活”为主题的居家体育锻炼活动，并实施锻炼时间目标管理．为确定一个合理的学生居家锻炼时间的完成目标，学校随机抽取了30名学生周累计居家锻炼时间（单位：h）的数据作为一个样本，并对这些数据进行了收集、整理和分析，过程如下：
【数据收集】
7 8 6 5 9 10 4 6 7 5 11 12 8 7 6
4 6 3 6 8 9 10 10 13 6 7 8 3 5 10
【数据整理】
将收集的30个数据按A，B，C，D，E五组进行整理统计，并绘制了如图所示的不完整的频数分布直方图（说明： ，其中t表示锻炼时间）；
【数据分析】
统计量 |
平均数 |
众数 |
中位数 |
锻炼时间（h） |
7.3 |
m |
7 |
请根据以上信息解答下列问题：
（1）填空：m＝ ；
（2）补全频数分布直方图；
（3）如果学校将管理目标确定为每周不少于7h，该校有600名学生，那么估计有多少名学生能完成目标？你认为这个目标合理吗？说明理由．
如图，在平面直角坐标系中，矩形ABCO的OA边在
轴上，OC边在
轴上，且B点坐标为（4，3）．动点M、N分别从点O、B同时出发，以1单位/秒的速度运动（点M沿OA向终点A运动，点N沿BC向终点C运动），过点N作NP∥AB交AC于点P，连结MP．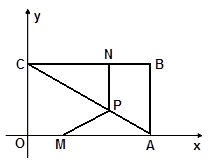
（1）直接写出OA、AB的长度；
（2）试说明△CPN∽△CAB；
（3）在两点的运动过程中，请求出ΔMPA的面积S与运动时间
的函数关系式；
（4）在运动过程中，△MPA的面积S是否存在最大值？若存在，请求出当为何值时有最大值，并求出最大值；若不存在，请说明理由．
已知：关于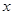
的方程
．
（1）若方程有两个相等的实数根，求
的值，并求出这时的根．
（2）问：是否存在正数，使方程的两个实数根的平方和等于136；若存在，请求出满足条件的值；若不存在，请说明理由．
某百货大搂服装柜在销售中发现：“七彩”牌童装平均每天可售出20件，每件盈利40元．为了迎接“元旦”，商场决定采取适当的降价措施，扩大销售量，增加盈利，减少库存．经市场调查发现：如果每件童装降价1元，那么平均每天就可多售出2件．
（1）要想平均每天销售这种童装盈利1200元，那么每件童装应降价多少元？
（2）用配方法说明：要想盈利最多，每件童装应降价多少元？
阅读下面的例题，请参照例题解方程
．
例：解方程
解：（1）当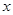
≥0时，原方程化为
，
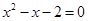解得：
（不合题意，舍去）．
（2）当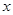＜0时，原方程化为
，
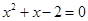解得：
（不合题意，舍去）．
∴原方程的根是
．
解方程
如图，四边形ABCD、DEFG都是正方形，连接AE、CG、AE与CG相交于点M，CG与AD相交于点N．
求证：（1）
；
（2）