小华同学学习函数知识后,对函数 通过列表、描点、连线,画出了如图1所示的图象.
x |
… |
|
|
|
|
|
|
|
|
|
|
|
… |
|
y |
… |
|
|
|
|
|
|
|
|
﹣4 |
|
|
|
… |
请根据图象解答:
(1)【观察发现】
①写出函数的两条性质:__________; __________;
②若函数图象上的两点 满足 ,则 一定成立吗? _____.(填“一定”或“不一定”)
(2)【延伸探究】如图2,将过 两点的直线向下平移 个单位长度后,得到直线 与函数 的图象交于点 ,连接 .
①求当 时,直线 的解析式和 的面积;
②直接用含 的代数式表示 的面积.

如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD.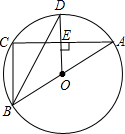
(1)求证:BD平分∠ABC;
(2) 当∠ODB=30°时,求证:BC="OD."
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(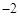 ,
,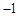 )、B(
)、B(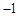 ,1)、C(0,
,1)、C(0, ).
).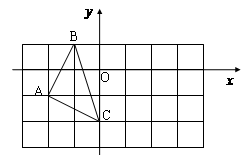
(1) 点B关于坐标原点O对称的点的坐标为__________;
(2) 将△ABC绕点C顺时针旋转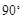 ,画出旋转后得到的△A1B1C;
,画出旋转后得到的△A1B1C;
(3) 求过点B1的反比例函数的解析式.
某渔船出海捕鱼,2010年平均每次捕鱼量为10吨,2012年平均每次捕鱼量为8.1吨,求2010年至2012年每年平均每次捕鱼量的年平均下降率.
解方程: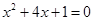
如图,在锐角三角形ABC中,BC=10,BC边上的高AM=6,D,E分别是边AB,AC上的两个动点(D不与A,B重合),且保持DE∥BC,以DE为边,在点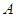 的异侧作正方形DEFG.
的异侧作正方形DEFG.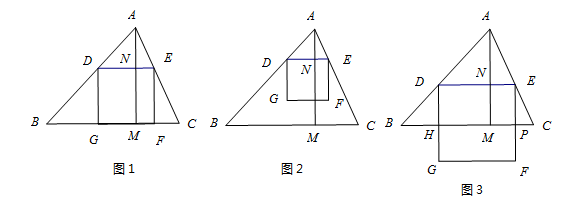
(1)因为,所以△ADE∽△ABC.
(2)如图1,当正方形DEFG的边GF在BC上时,求正方形DEFG的边长;
(3)设DE = x,△ABC与正方形DEFG重叠部分的面积为y.
①如图2,当正方形DEFG在△ABC的内部时,求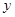 关于
关于 的函数关系式,写出x的取值范围;
的函数关系式,写出x的取值范围;
②如图3,当正方形DEFG的一部分在△ABC的外部时,求 关于
关于 的函数关系式,写出x的取值范围;
的函数关系式,写出x的取值范围;
③当x为何值时,y有最大值,最大值是多少?