小红看到一处喷水景观，喷出的水柱呈抛物线形状，她对此展开研究：测得喷水头 距地面 ，水柱在距喷水头 水平距离 处达到最高，最高点距地面 ；建立如图所示的平面直角坐标系，并设抛物线的表达式为 ，其中 是水柱距喷水头的水平距离， 是水柱距地面的高度．
（1）求抛物线的表达式．
（2）爸爸站在水柱正下方，且距喷水头 水平距离 ．身高 的小红在水柱下方走动，当她的头顶恰好接触到水柱时，求她与爸爸的水平距离．
已知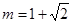
，
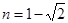，求（1）
,
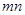的值；（2）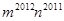
的值；（3）
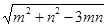的值.
已知：a.b.c满足
,求：
（1）a,b,c的值；
（2）试问以a,b,c为边能否构成三角形？若能构成三角形，求出三角形的周长；若不能构成三角形，请说明理由.
先化简，再求值：
，其中
.
计算
（1）
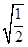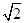（2）2
－
－(
＋
－2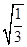
)
（3）
; (a＞0,b＞0)
（4）
＋(－5＋3
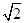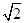)(―5―3)
如图，在边长为4的正方形ABCD中，点P在AB上从A向B运动，连接DP交AC于点Q．
（1）试证明：无论点P运动到AB上何处时，都有△ADQ≌△ABQ；
（2）当点P在AB上运动到什么位置时，△ADQ的面积是正方形ABCD面积的
；
（3）若点P从点A运动到点B，再继续在BC上运动到点C，在整个运动过程中，当点P运动到什么位置时，△ADQ恰为等腰三角形．