如图,抛物线 与 轴交于 两点,与 轴交于 点, .

(1)求拋物线的解析式;
(2)在第二象限内的拋物线上确定一点 ,使四边形 的面积最大,求出点 的坐标;
(3)在(2)的结论下,点 为 轴上一动点,抛物线上是否存在一点 ,使点 为顶点的四边形是平行四边形,若存在,请直接写出 点的坐标;若不存在,请说明理由.
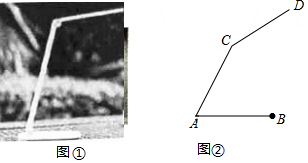
图①是放置在水平面上的台灯,图②是其侧面示意图(台灯底座高度忽略不计),其中灯臂 ,灯罩 ,灯臂与底座构成的 . 可以绕点 上下调节一定的角度.使用发现:当 与水平线所成的角为 时,台灯光线最佳.现测得点 到桌面的距离为 .请通过计算说明此时台灯光线是否为最佳?(参考数据: 取 .
已知:在 中, .
(1)求作: 的外接圆.(要求:尺规作图,保留作图痕迹,不写作法)
(2)若 的外接圆的圆心 到 边的距离为4, ,则 .

小甘到文具超市去买文具.请你根据如图中的对话信息,求中性笔和笔记本的单价分别是多少元?

二次函数 的图象交 轴于点 , 两点,交 轴于点 .动点 从点 出发,以每秒2个单位长度的速度沿 方向运动,过点 作 轴交直线 于点 ,交抛物线于点 ,连接 ,设运动的时间为 秒.

(1)求二次函数 的表达式;
(2)连接 ,当 时,求 的面积;
(3)在直线 上存在一点 ,当 是以 为直角的等腰直角三角形时,求此时点 的坐标;
(4)当 时,在直线 上存在一点 ,使得 ,求点 的坐标.
通过对下面数学模型的研究学习,解决问题.
【模型呈现】
如图,在 , ,将斜边 绕点 顺时针旋转 得到 ,过点 作 于点 ,可以推理得到 ,进而得到 , .
我们把这个数学模型称为“ 型”.
推理过程如下:

【模型应用】
如图,在 内接于 , , ,将斜边 绕点 顺时针旋转一定的角度得到 ,过点 作 于点 , , ,连接 交 于点 .
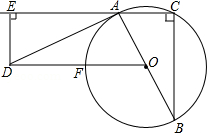
(1)求证: 是 的切线;
(2)连接 交 于点 ,连接 .求证: .