如图，锐角△ABC中，∠A,∠B,∠C的对边分别是a,b,c-优题课

题文

如图，锐角 $△ ABC$ 中， $∠ A, ∠ B, ∠ C$ 的对边分别是 $a, b, c$ ，已知二次函数 $y = x^{2} cos A - x + \frac{1}{cos A}$ 的图象顶点与点 $(- 2 cos A, 3 cos A)$ 关于 $y$ 轴对称.延长 $AB$ 至 $P$ 点，使 $AP = 2 AC$ ，且以 $C$ 为圆心， $AC$ 为半径的圆与以 $B$ 为圆心 $BP$ 为半径的圆相外切.

（1）求 $∠ A$ 的度数;

（2）设 $BP = r$ ，求 $a : b : c$ 的值;

（3）若关于 $t$ 的方程 $3 t^{2} - 3 ct + (a + b) = 0$ 的两个根 $α, β$ 满足 $α (α + 1) + β (β + 1) = (α + 1) (β + 1)$ ，求 $△ ABC$ 的面积.

科目数学题型解答题难度中等

登录免费查看答案和解析

相关试题

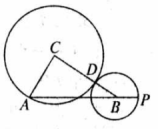
如图，已知AB是⊙O的直径，直线CD与⊙O相切于点C，AC平分∠DAB．

（1）求证：AD⊥DC；
（2）若AD=2，AC=，求AB的长．

已知矩形ABCD的一条边AD=8，将矩形ABCD折叠，使得顶点B落在CD边上的P点处．如图，已知折痕与边BC交于O，连结AP、OP、OA．

（1）求证：△OCP∽△PDA；
（2）若△OCP与△PDA的面积比为1：4，求边AB的长；

如图，在△ABC中，AD是角平分钱，点E在AC上，且∠EAD=∠ADE．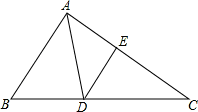

（1）求证：△DCE∽△BCA；
（2）若AB=3，AC=4．求DE的长．

一不透明的袋子中装有4个球，它们除了上面分别标有的号码l、2、3、4不同外，其余均相同。将小球搅匀，并从袋中任意取出一球后放回；再将小球搅匀，并从袋中再任意取出一球。求第二次取出球的号码比第一次的大的概率。（请用“画树状图”或“列表”的方法给出分析过程，并写出结果）

某校八年级学生开展踢毽子比赛活动，每班派5名学生参加，按团体总分多少排列名次，在规定时间内每人踢100个以上（含100）为优秀．下表是成绩最好的甲班和乙班5名学生的比赛数据（单位：个）：

	1号	2号	3号	4号	5号	总数
甲班	89	100	96	118	97	500
乙班	100	95	110	91	104	500

经统计发现两班总数相等．此时有学生建议，可以通过考察数据中的其他信息作为参考．
请你回答下列问题：
（1）计算两班的优秀率．
（2）求两班比赛成绩的中位数．
（3）比较两班比赛数据的方差哪一个小．
（4）根据以上三条信息，你认为应该把冠军奖杯发给哪一个班级？简述你的理由．

试卷网试题网古诗词网作文网范文网