口袋中有4个相同的小球，它们分别写有数字2,3,4,5，从口-优题课

题文

口袋中有 $4$ 个相同的小球，它们分别写有数字 $2, 3, 4, 5$ ，从口袋中随机取出两个球，用所得的两个数 $a$ 和 $b$ 构成函数 $y = ax - 2$ 和 $y = x + b$ ，求使这两个函数的交点在直线 $x = 2$ 右侧的概率.

科目数学题型解答题难度中等

登录免费查看答案和解析

相关试题

如图，在平面直角坐标系中，点A、B的坐标分别为（-5，0）和（5，0），以AB为直径在x轴的上方作半圆O，点C是该半圆上第一象限内的一个动点，连结AC、BC，并延长BC至点D，使BC=CD，过点D作x轴的垂线，分别交x轴、线段AC于点E、F，E为垂足，连结OF．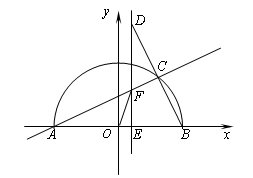

（1）当∠CAB=30°时，求弧BC的长；
（2）当AE=6时，求弦BC的长；
（3）在点C运动的过程中，是否存在以点O、E、F为顶点的三角形与△DEB相似？若存在，请求出此时E点的坐标；若不存在，请说明理由．

如图，在⊙O的内接△ABC中，AD⊥BC于D，

（1）①若作直径AP，求证：AB·AC＝AD·AP；
②已知AB＋AC＝12，AD＝3，设⊙O的半径为y，AB的长为x．求y与x的函数关系式，及自变量x的取值范围；
（2）图2中，点E为⊙O上一点，且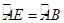，求证：CE＋CD＝BD.

三个小球分别标有﹣2，0，1三个数，这三个球除了标的数不同外，其余均相同，将小球放入一个不透明的布袋中搅匀．
（1）从布袋中任意摸出一个小球，将小球上所标之数记下，然后将小球放回袋中，搅匀后再任意摸出一个小球，再记下小球上所标之数，求两次记下之数的和大于0的概率．（请用“画树状图”或“列表”等方法给出分析过程，并求出结果）
（2）从布袋中任意摸出一个小球，将小球上所标之数记下，然后将小球放回袋中，搅匀后再任意摸出一个小球，将小球上所标之数再记下，…，这样一共摸了13次．若记下的13个数之和等于﹣4，平方和等于14．求：这13次摸球中，摸到球上所标之数是0的次数．

已知：如图，矩形ABCD中，CD＝2，AD＝3，以C点为圆心，作一个动圆，与线段AD交于点P（P和A、D不重合），过P作⊙C的切线交线段AB于F点.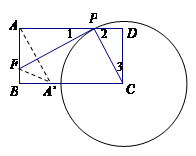

（1）求证：△CDP∽△PAF；
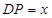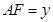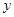（2）设，，求关于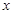的函数关系式，及自变量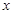的取值范围；
（3）是否存在这样的点P，使△APF沿PF翻折后，点A落在BC上，请说明理由.

如图，AB是半圆O的直径，C、D是半圆O上的两点，且OD∥BC，OD与AC交于点E．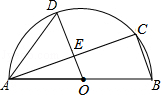

（1）若∠B=70°，求∠CAD的度数；
（2）若AB=4，AC=3，求DE的长．

试卷网试题网古诗词网作文网范文网