先阅读再化简求值.
(1)在化简 的过程中,小王和小李的化简结果不一样.
小王的化简过程如下:
原式 .
小李的化简过程如下:
原式 .
请判断谁的化简结果正确,并说明理由.
(2)化简求值:已知 ,求 的值(结果保留根号).
实践应用(本小题满分6分)
国家教育部规定“中小学生每天在校体育活动时间不低于1小时”.2012年,为了了解我市毕业班学生体育活动情况,随机对我市240名毕业班学生进行调查,调查内容为:
以下是根据所得的数据制成的统计图的一部分.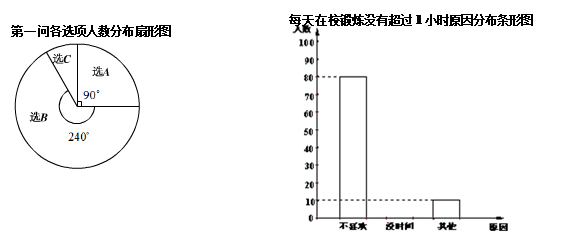
问题:根据以上信息,解答下列问题:
(1)每天在校锻炼时间超过1小时的人数是▲;
(2)请将条形图补充完整;
(3)2011年我市初中毕业生约为8.4万人,请你估计今年全市初中毕业生中每天锻炼时间低于0.5小时的学生约有多少万人?
推理证明(本小题满分6分)
如图,已知AB=AC,AD=AE.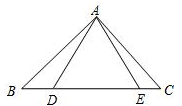
求证:BD=CE.
运算求解(本小题满分10分)
(1)解不等式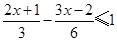 ,并把它的解集在数轴上表示出来.
,并把它的解集在数轴上表示出来.
(2)解方程: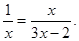
计算化简(本小题满分10分)
(1)计算: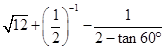
(2)化简: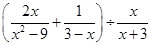 ,然后选择一个合适的
,然后选择一个合适的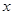 的值代入上式求值.
的值代入上式求值.
如图,在△ABC中,AC = BC,AB = 8,CD⊥AB,垂足为点D.M为边AB上任意一点,点N在射线CB上(点N与点C不重合),且MC = MN.设AM = x.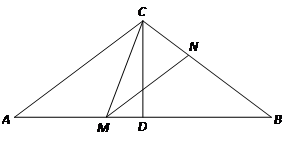
(1)如果CD = 3,AM = CM,求AM的长;
(2)如果CD = 3,点N在边BC上.设CN = y,求y与x的函数解析式,并写出函数的定义域;
(3)如果∠ACB = 90°,NE⊥AB,垂足为点E.当点M在边AB上移动时,试判断线段ME的长是否会改变?说明你的理由.