如图。（1）如图①以△ABC的边AB,AC为边分别向外作正方-优题课

游客

题文

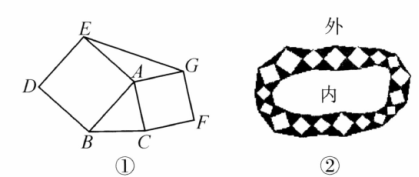
如图。（1）如图①以 $△ ABC$ 的边 $AB, AC$ 为边分别向外作正方形 $ABDE$ 和正方形 $ACFG$ ，连接 $EG$ ，试判断 $△ ABC$ 与 $△ AEG$ 面积之间的关系，并说明理由.

（2）园林小路，曲径通幽，如图②所示。小路由白色的正方形大理石和黑色的三角形大理石铺成.已知中间的所有正方形的面积之和是 $a m^{2}$ ，内圈的所有三角形的面积之和是 $b m^{2}$ ，这条小路一共占地多少 $m^{2}$ ?

科目数学题型解答题难度中等

登录免费查看答案和解析

相关试题

化简：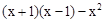

计算：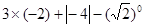

抛物线与x轴交于A，B两点（点A在点B左侧），与y轴交于点C，点D为顶点．

（1）求点B及点D的坐标．
（2）连结BD，CD，抛物线的对称轴与x轴交于点E．
①若线段BD上一点P，使∠DCP=∠BDE，求点P的坐标．
②若抛物线上一点M，作MN⊥CD，交直线CD于点N，使∠CMN=∠BDE，求点M的坐标．

在△ABC中，∠CAB=90°，AD⊥BC于点D，点E为AB的中点，EC与AD交于点G，点F在BC上．

（1）如图1，AC：AB=1：2，EF⊥CB，求证：EF=CD．
（2）如图2，AC：AB=1：，EF⊥CE，求EF：EG的值．

若一个矩形的一边是另一边的两倍，则称这个矩形为方形，如图1，矩形ABCD中，BC=2AB，则称ABCD为方形．

（1）设a，b是方形的一组邻边长，写出a，b的值（一组即可）．
（2）在△ABC中，将AB，AC分别五等分，连结两边对应的等分点，以这些连结为一边作矩形，使这些矩形的边B₁C₁，B₂C₂，B₃C₃，B₄C₄的对边分别在B₂C₂，B₃C₃，B₄C₄，BC上，如图2所示．
①若BC=25，BC边上的高为20，判断以B₁C₁为一边的矩形是不是方形？为什么？
②若以B₃C₃为一边的矩形为方形，求BC与BC边上的高之比．

试卷网试题网古诗词网作文网范文网