如图所示, 为线段 上一动点,分别过点 作 , ,连接 .已知 ,设 .
(1)用含 的代数式表示 的长;
(2)请问点 满足什么条件时, 的值最小?
(3)根据(2)中的规律和结论,请构图求出代数式 的最小值.

如图1,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=5,OC=4.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,边AE上有一动点P(不与A,E重合)自A点沿AE方向向E点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为t秒(0<t<5),过P点作ED的平行线交AD于点M,过点M作AE的平行线交DE于点N.
(1)直接写出 D,E 两点的坐标,D( ),E( )
(2)求四边形PMNE的面积S与时间t之间的函数关系式;当t取何值时,S有最大值?
(3)当t为何值时,DP平分∠EDA?
(4)当t为何值时,以A,M,E为顶点的三角形为等腰三角形,并求出相应的时刻点M的坐标.
问题情境
如图,在x轴上有两点A(m,0),B(n,0)(n>m>0).分别过点A,点B作x轴的垂线,交抛物线y=x2于点C、点D.直线OC交直线BD于点E,直线OD交直线AC于点F,点E、点F的纵坐标分别记为yE,yF.
特例探究
填空:
当m=1,n=2时,yE= ,yF= ;
当m=3,n=5时,yE= ,yF= .
归纳证明
对任意m,n(n>m>0),猜想yE与yF的大小关系,并证明你的猜想.
拓展应用
(1)若将“抛物线y=x2”改为“抛物线y=ax2(a>0)”,其他条件不变,请直接写出yE与yF的大小关系;
(2)连接EF,AE.当S四边形OFEB=3S△OFE时,直接写m与n的大小关系及四边形OFEA的形状.
进入冬季,我市空气质量下降,多次出现雾霾天气.商场根据市民健康需要,代理销售一种防尘口罩,进货价为20元/包,经市场销售发现:销售单价为30元/包时,每周可售出200包,每涨价1元,就少售出5包.若供货厂家规定市场价不得低于30元/包,且商场每周完成不少于150包的销售任务.
(1)试确定周销售量y(包)与售价x(元/包)之间的函数关系式;
(2)试确定商场每周销售这种防尘口罩所获得的利润w(元)与售价x(元/包)之间的函数关系式,并直接写出售价x的范围;
(3)当售价x(元/包)定为多少元时,商场每周销售这种防尘口罩所获得的利润w(元)最大?最大利润是多少?
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上.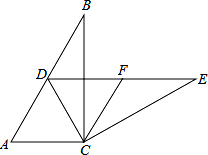
(1)求n的值;
(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.
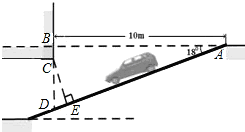
某居民小区为缓解居民停车难问题为缓解“停车难”问题,拟造地下停车库,如图是地下停车库坡道入口的设计示意图,其中,AB⊥BD,∠BAD=18°,C在BD上,BC=0.5.根据规定,地下停车库破道口上方要张贴限高标志,以便告知驾驶员所驾车辆能否安全驶入.请根据以上数据,求出该地下停车库限高CE的长.(结果精确到0.1米)
(sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)