已知关于 的方程 有三个解,求 的取值范围.
如图(7),已知线段a和b,求作一个直角三角形,使它的两条直角边分别等于线段a和b.(不要求写作法,但要保留作图痕迹。)
解方程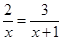
 =
=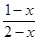
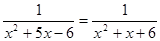
化简


等腰直角△ABC和⊙O如图放置,已知AB=BC=1,∠ABC=90°,⊙O的半径为1,圆心O与直线AB的距离为5.现△ABC以每秒2个单位的速度向右移动,同时△ABC的边长AB、BC又以每秒0.5个单位沿BA、BC方向增大.
⑴ 当△ABC的边(BC边除外)与圆第一次相切时,点B移动了多少距离?
⑵ 若在△ABC移动的同时,⊙O也以每秒1个单位的速度向右移动,则△ABC从开始移动,到它的边与圆最后一次相切,一共经过了多少时间?
⑶ 在⑵的条件下,是否存在某一时刻,△ABC各边刚好与⊙O都相切?若存在,求出刚好符合条件时两个图形移动了多少时间?若不存在,能否改变AB、BC沿BA、BC方向的速度,使△ABC各边刚好与⊙O都相切.
如图,在平面直角坐标中,边长为2的正方形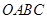 的两顶点
的两顶点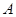 、
、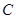 分别在
分别在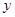 轴、
轴、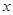 轴的正半轴上,点
轴的正半轴上,点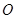 在原点.现将正方形
在原点.现将正方形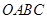 绕
绕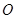 点顺时针旋转,旋转角为θ,当
点顺时针旋转,旋转角为θ,当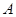 点第一次落在直线
点第一次落在直线 上时停止旋转.旋转过程中,
上时停止旋转.旋转过程中,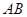 边交直线
边交直线 于点
于点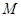 ,
,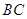 边交
边交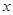 轴于点
轴于点 .
.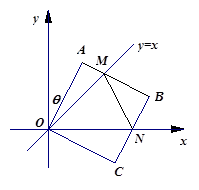
(1)当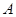 点第一次落在直线
点第一次落在直线 上时,求A、B两点坐标(直接写出结果);
上时,求A、B两点坐标(直接写出结果);
(2)设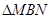 的周长为
的周长为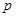 ,在旋转正方形
,在旋转正方形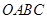 的过程中,
的过程中,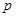 值是否有变化?请证明你的结论.
值是否有变化?请证明你的结论.