等腰直角△ABC和⊙O如图放置,已知AB=BC=1,∠ABC=90°,⊙O的半径为1,圆心O与直线AB的距离为5.现△ABC以每秒2个单位的速度向右移动,同时△ABC的边长AB、BC又以每秒0.5个单位沿BA、BC方向增大.
⑴ 当△ABC的边(BC边除外)与圆第一次相切时,点B移动了多少距离?
⑵ 若在△ABC移动的同时,⊙O也以每秒1个单位的速度向右移动,则△ABC从开始移动,到它的边与圆最后一次相切,一共经过了多少时间?
⑶ 在⑵的条件下,是否存在某一时刻,△ABC各边刚好与⊙O都相切?若存在,求出刚好符合条件时两个图形移动了多少时间?若不存在,能否改变AB、BC沿BA、BC方向的速度,使△ABC各边刚好与⊙O都相切.
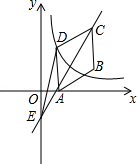
如图,在平行四边形 中,点 、 、 的坐标分别是 、 、 ,双曲线 过点 .
(1)求双曲线的解析式;
(2)作直线 交 轴于点 ,连接 ,求 的面积.
如图,在 中,点 是直径 延长线上一点,过点 作 的切线,切点为 ,连接 .
(1)求证: ;
(2)若 平分 ,且分别交 、 于点 、 ,当 时,求 的长.

某大型企业为了保护环境,准备购买 、 两种型号的污水处理设备共8台,用于同时治理不同成分的污水,若购买 型2台、 型3台需54万,购买 型4台、 型2台需68万元.
(1)求出 型、 型污水处理设备的单价;
(2)经核实,一台 型设备一个月可处理污水220吨,一台 型设备一个月可处理污水190吨,如果该企业每月的污水处理量不低于1565吨,请你为该企业设计一种最省钱的购买方案.
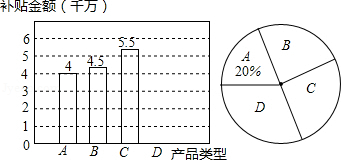
近几年来, 国家对购买新能源汽车实行补助政策, 2016 年某省对新能源汽车中的“插电式混合动力汽车”实行每辆 3 万元的补助, 小刘对该省 2016 年“纯电动乘用车”和“插电式混合动力车”的销售计划进行了研究, 绘制出如图所示的两幅不完整的统计图 .
(1) 补全条形统计图;
(2) 求出“ ”所在扇形的圆心角的度数;
(3) 为进一步落实该政策, 该省计划再补助 4.5 千万元用于推广上述两大类产品, 请你预测, 该省 16 年计划大约共销售“插电式混合动力汽车”多少辆?
注: 为纯电动续航行驶里程, 图中 表示“纯电动乘用车” , 表示“纯电动乘用车” , 表示“纯电动乘用车” , 为“插电式混合动力汽车” .
如图,已知二次函数 过 , 两点.
(1)求二次函数 的解析式;
(2)将 沿 轴翻折,再向右平移2个单位,得到抛物线 ,直线 交 于 、 两点,求线段 的长度(用含 的代数式表示);
(3)在(2)的条件下, 、 交于 、 两点,如果直线 与 、 的图象形成的封闭曲线交于 、 两点 在左侧),直线 与 、 的图象形成的封闭曲线交于 、 两点 在左侧),求证:四边形 是平行四边形.
