问题探究:
(1)请你在图①中做一条直线,使它将矩形 分成面积相等的两部分;
(2)如图②,点 是矩形 内一点,请你在图②中过 点作一条直线,使它将矩形 分成面积相等的两部分.
问题解决:
(3)如图③,在平面直角坐标系 中,多边形 的顶点坐标分别是 .若直线 经过点 ,且将多边形 分割成面积相等的两部分,求直线 的函数表达式.

如图所示,在△ABC中,AC=8,BC=6,在△ABC中,DE为AB边上的高,DE=12,△ABE的面积为60,△ABC是否为直角三角形?说明理由.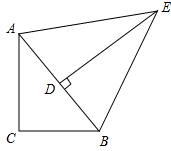
如图,在四边形ABCD中,∠C=90°,AB=13,BC=4,CD=3,AD=12.
(1)AD⊥BD吗?为什么?
(2)求四边形ABCD的面积.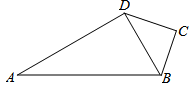
张老师在一次“探究性学习”课中,设计了如下数表:
| n |
2 |
3 |
4 |
5 |
… |
| a |
22-1 |
32-1 |
42-1 |
52-1 |
… |
| b |
4 |
6 |
8 |
10 |
… |
| c |
22+1 |
32+1 |
42+1 |
52+1 |
… |
(1)请你分别观察a,b,c与n之间的关系,并用含自然数n(n>1)的代数式表示:
a=_______,b= _______,c=_______;
(2)猜想:以a,b,c为边的三角形是否为直角三角形并证明你的猜想.
下列各数中,哪些是有理数?哪些是无理数?
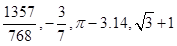 .
.
在: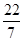 ,
,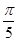 ,0,3.14,
,0,3.14, ,
,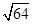 ,7.151551…(每相邻两个“1”之间依次多一个“5”)中,
,7.151551…(每相邻两个“1”之间依次多一个“5”)中,
整数集合{ …},
分数集合{ …},
无理数集合{ …}.