如图,从如图①所示的等边三角形开始,把它各边分成相等的三段,在中间一段上向外画出一个小等边三角形,形成如图②所示的六角星图形;再在六角星各边上用同样的方法向外画出更小的等边三角形,形成如图③所示的有 个尖角的图形,然后,在其各边上再用同样的方法向外画出更小的等边三角形如图④,如此继续下去,图形的轮廓就能形成分支越来越多的曲线,这就是瑞典数学家科赫将雪花理想化得到的科赫雪花曲线.

如果设原等边三角形的边长为 ,不妨把每一次图形的变化过程叫做“生长”,例如第一次生长后得到图②,每个小等边三角形的边长为 ,所形成的图形的周长为 ,请填写下表(用含 的代数式表示).
第一次生长后 |
第二次生长后 |
第三次生长后 |
… |
第 次生长后 |
|
每个小等边三角形的边长 |
|
… |
|||
所形成图形的周长 |
|
… |
如图,在平面直角坐标系中, 的顶点 是坐标原点,点 的坐标为 ,点 的坐标为 ,动点 从 开始以每秒1个单位长度的速度沿 轴正方向运动,设运动的时间为 秒 ,过点 作 轴,分别交 , 于点 , .
(1)填空: 的长为 , 的长为 ;
(2)当 时,求点 的坐标;
(3)请直接写出 的长为 (用含 的代数式表示);
(4)点 是线段 上一动点(点 不与点 , 重合), 和 的面积分别表示为 和 ,当 时,请直接写出 (即 与 的积)的最大值为 .
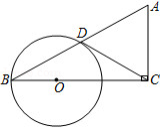
如图,在 中, ,点 为 边上一点,以点 为圆心, 长为半径的圆与边 相交于点 ,连接 ,当 为 的切线时.
(1)求证: ;
(2)若 , 的半径为1,请直接写出 的长为 .
某工程队准备修建一条长 的盲道,由于采用新的施工方式,实际每天修建盲道的长度比原计划增加 ,结果提前2天完成这一任务,原计划每天修建盲道多少米?
某市为了将生活垃圾合理分类,并更好地回收利用,将垃圾分为可回收物、厨余垃圾、有害垃圾和其他垃圾四类.现随机抽取该市 吨垃圾,将调查结果制成如下两幅不完整的统计图:
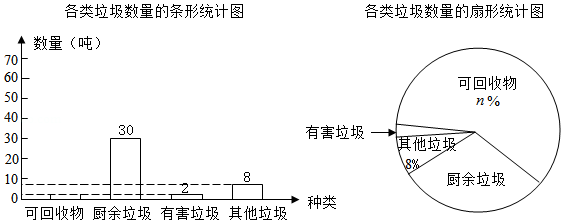
根据统计图提供的信息,解答下列问题:
(1) , ;
(2)根据以上信息直接补全条形统计图;
(3)扇形统计图中,厨余垃圾所对应的扇形圆心角的度数为 度;
(4)根据抽样调查的结果,请你估计该市2000吨垃圾中约有多少吨可回收物.
如图,在矩形 中,对角线 的垂直平分线分别与边 和边 的延长线交于点 , ,与边 交于点 ,垂足为点 .
(1)求证: ;
(2)若 , ,请直接写出 的长为 .