设 , 都是有理数, 是无理数.求证:
(1)当 时, 是有理数;
(2)当 时, 是无理数.
【提出问题】
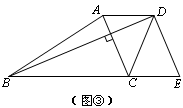
如图①,在梯形ABCD中,AD//BC,AC、BD交于点E,∠BEC=n°,若AD=a,BC=b,则梯形ABCD的面积最大是多少?
【探究过程】
小明提出:可以从特殊情况开始探究,如图②,在梯形ABCD中,AD//BC,AC⊥BD,若AD=3,BC=7,则梯形ABCD的面积最大是多少?
如图③,过点D做DE//AC交BC的延长线于点E,那么梯形ABCD的面积就等于△DBE的面积,求梯形ABCD的面积最大值就是求△DBE的面积最大值.如果设AC=x,BD=y,那么S△DBE=xy.
以下是几位同学的对话:
A同学:因为y=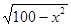 ,所以S△DBE=x
,所以S△DBE=x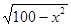 ,求这个函数的最大值即可.
,求这个函数的最大值即可.
B同学:我们知道x2+y2=100,借助完全平方公式可求S△DBE=xy的最大值
C同学:△DBE是直角三角形,底BE=10,只要高最大,S△DBE就最大,我们先将所有满足BE=10的直角△DBE都找出来,然后在其中寻找高最大的△DBE即可.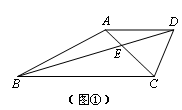
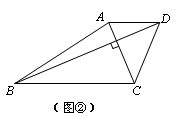
(1)请选择A同学或者B同学的方法,完成解题过程.
(2)请帮C同学在图③中画出所有满足条件的点D,并标出使△DBE面积最大的点D1.(保留作图痕迹,可适当说明画图过程)
【解决问题】
根据对特殊情况的探究经验,请在图①中画出面积最大的梯形ABCD的顶点D1,并直接写出梯形ABCD面积的最大值.
阅读:
如图①,已知:正方形ABCD,面积为a,点E、F、G、H分别是AB、BC、CD、DA边的中点,连接AG、BH、CE、DF,求四边形MNPQ的面积.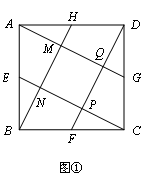
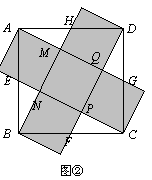
小明提出了如下的解决办法:如图②,分别将△AMH、△BNE、△CPF、△DQG分割并拼补成一个与正方形ABCD面积相等的新图形.
请你参考小明同学解决问题的方法,利用图形变换解决下列问题:
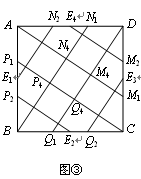
如图③,在正方形ABCD中,E1、E2、E3、E4分别为AB、BC、CA、DA的中点,P 1、P2, Q1、Q2,M 1、M2,N1、N2分别为AB、BC、CA、DA的三等分点.
(1)在图③中画出一个和正方形ABCD面积相等的新图形,并用阴影表示(保留画图痕迹);
(2)图③中四边形P4Q4M4N4的面积为.
如图,四边形ABCD是平行四边形,AB=2,以边AB为直径的⊙O经过点D,且∠DAB=45°.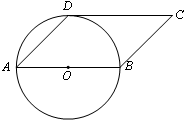
(1)试判断CD与⊙O的位置关系,并说明理由;
(2)若以C为圆心的⊙C与⊙O 相切,求⊙C的半径.
甲、乙两地相距20千米.小明上午8:30骑自行车由甲地去乙地,平均车速8千米/小时;小丽上午10:00坐公共汽车沿相同的路线也由甲地去乙地,平均车速为40千米/小时.
(1)分别写出两人离甲地的距离与时间的函数关系式,并在同一平面直角坐标系中画出两个函数的图象;
(2)判断谁先到达乙地,并说明理由.
如图,大楼AB、CD和大树EF的底端B、D、F在同一直线上,BF=FD=10米,AB=16米,某人在楼顶A处测得点C的仰角为22°,测得点E的俯角为45°.(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40)
(1)求大树EF的高度;
(2)求大楼CD的高度.