如图,在平面直角坐标系中已知点 ,四边形 是长方形,点 从 运动,速度为 (单位 ).

(1)当 在 上运动时,直线 能否将长方形 的面积分为 两部分,若能,求 点坐标,若不能,说明理由;
(2)点 运动到 时,何时 的面积等于 矩形面积?并求此时 点坐标.
画出面积相等的长方形、三角形、平行四边形和梯形各一个.
如果每一个小正方形的面积是1平方厘米,我画的图形的面积都是 平方厘米.
直角三角形ABC的三条边分别是5cm,3cm和4cm,其中AC=4CM,将它的直角边AC对折到斜边AB上,使AC与AD重合,则图中阴影部分的编辑是多少平方厘米?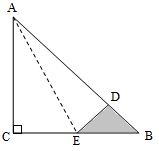
如下图,ABCD是一个边长为6米的正方形模拟跑道,甲玩具车从A出发顺时针行进,速度是每秒5厘米,同时乙玩具车从CD的中点E处出发逆时针行进,结果两车第二次相遇恰好是在B点,求乙车每秒走多少厘米?
下面是商家的一则促销信息。
(1)此次活动的中奖率是()%。
(2)此次活动的奖金共()元。
(3)如果每台加湿器的进货价是150元,商家在这次促销活动中赚的钱是进货价的百分之几?(列式计算)(百分号前保留两位小数)
建筑工地有一圆锥形沙堆,量得底面直径是2米,高是1.5米。如果用容积是0.36立方米的车子把这堆沙子运走,至少需要运几次?