(本 题满分14分,第(1)、(2)小题每小题满分5分,第(3)小题
题满分14分,第(1)、(2)小题每小题满分5分,第(3)小题
 满分4分)
满分4分)
已知,在边长为6的正方形ABCD的两侧如图作正方形BEFG、正方形DMNK,恰好使得N、A、F三点在一直线上,联结M F交线段AD于点P,联结NP,设正方形BEFG的边长为x,正方形DMNK的边长为y,
F交线段AD于点P,联结NP,设正方形BEFG的边长为x,正方形DMNK的边长为y,
(1)求y关于x的函数关系式及自变量x的取值范围;
(2)当△NPF的面积为32时,求x的值;
(3)以P为圆心,AP为半径的圆能否与以G为圆心,GF为半径的圆相切,若能请求x的值,若不能,请说明理由。
我们容易发现:反比例函数的图象是一个中心对称图形,你可以利用这一结论解决问题。如图,在同一直角坐标系中,正比例函数的图象可以看作是将x轴所在的直线绕着原点O逆时针旋转 度后的图形。它与反比例函数
度后的图形。它与反比例函数 的图象分别交于第一、三象限的点B、D,已知点A(-m,0)、C(m,0)。
的图象分别交于第一、三象限的点B、D,已知点A(-m,0)、C(m,0)。
(1)判断并填写,不论 取何值,四边形ABCD的形状一定是______;
取何值,四边形ABCD的形状一定是______;
(2)①当点B坐标为(p,1)时,四边形ABCD是矩形,试求p、 和m的值;
和m的值;
②观察猜想:对①中的m值,能使四边形ABCD为矩形的点B共有几个?(不必说理)
(3)试探究:四边形ABCD能不能是菱形?若能,直接写出B点的坐标;若不能,说明理由。
学完“证明(二)”一章后,老师布置了一道思考题:如图,点M、N分别在正三角形ABC的边BC.CA上,且BM=CN,AM、BN交于点Q。求证:∠BQM=60°。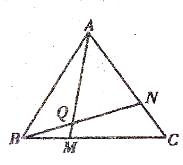
(1)请你完成这道思考题;
(2)做完(1)后,同学们在老师的启发下进行了反思,提出了许多问题,如:
①若将题中“BM=CN”与“∠BQM=60°”的位置交换,得到的是否仍是真命题?
②若将题中的点M,N分别移动到BC,CA的延长线上,是否仍能得到∠BQM=60°?
③若将题中的条件“点M,N分别在正三角形ABC的BC、CA边上”改为“点M,N分别在正方形ABCD的BC,CD边上”,是否仍能得到∠BQM=60°?对②,③进行证明。(自己画出对应的图形)
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(4,2),过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N。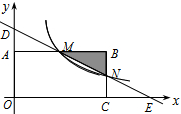
(1)求直线DE的解析式和点M的坐标;
(2)若反比例函数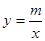 (x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上;
(x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上;
(3)若反比例函数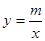 (x>0)的图象与△MNB有公共点,请直接写出m的取值范围。
(x>0)的图象与△MNB有公共点,请直接写出m的取值范围。
如图,△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=2,DC=3,求AD的长。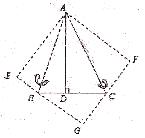
小萍同学灵活运用了轴对称知识,将图形进行翻折变换,巧妙地解答了此题。
(1)分别以AB、AC为对称轴,画出△ABD、△ACD的轴对称图形,D、C点的对称点分别为E、F,延长EB、FC相交于G点,求证:四边形AEGF是正方形;
(2)设AD=x,利用勾股定理,建立关于x的方程模型,求出x的值。
如图,矩形ABCD中,P是线段AD上一动点,O为BD中点,PO的延长线交BC于Q。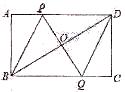
(1)求证:四边形PDQB为平行四边形;
(2)若AD=8cm,AB=6cm,P从点A出发,以1cm/秒的速度向D运动(不与D重合)。设点P运动时间为t秒,请用t表示PD的长,并求t为何值时,四边形PBQD是菱形。