如图，△ABC中，已知∠BAC=45°，AD⊥BC于D，BD=2，DC=3，求AD的长。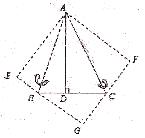
小萍同学灵活运用了轴对称知识，将图形进行翻折变换，巧妙地解答了此题。
（1）分别以AB、AC为对称轴，画出△ABD、△ACD的轴对称图形，D、C点的对称点分别为E、F，延长EB、FC相交于G点，求证：四边形AEGF是正方形；
（2）设AD=x，利用勾股定理，建立关于x的方程模型，求出x的值。
【原创】去年我市教育局开展了认领“文明清单”活动，今年开学为落实认领“文明清单”活动，我校初一、初二两个年组对活动情况进行了统计，落实后的清单条数由落实前的清单条数与落实后认领的条数两部分组成（已知落实前每个年组的清单条数相同，落实后人均条数一样），下表是初一、初二的学生数及落实后清单条数的情况信息：
| 初一 |
初二 |
初三 |
|
| 人数 |
200 |
180 |
210 |
| 清单总数（条） |
1800 |
1700 |
（1）试求落实前各年组的清单总数及落实后人均认领清单条数？
（2）如果初三年组想要清单条数达到2480条，那么初三年组人均应该认领多少条？
若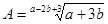
是
的算术平方根，
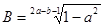为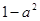
的立方根，求
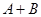的立方根；
三角形ABC与三角形A’B’C’在平面直角坐标系中的位置如图．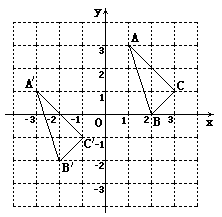
（1）分别写出下列各点的坐标：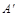
； 
；
；
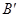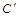（2）说明三角形A’B’C’由三角形ABC经过怎样的平移得到 ．
（3）若点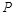
（
，
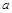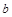）是 三角形ABC内部一点，则平移后三角形A’B’C’内的对应点
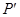的坐标为 ；
（4）求三角形ABC的面积．
【改编】将一副三角板拼成如图1所示的图形，过点C作CF平分∠DCE交DE于点F．
（1）试确定CF与AB的位置关系并说明理由．
（2）∠DFC= °．
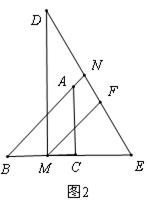
（3）若如图2、图3所示放置两个三角板时，设BA与DE交于点N，试确定∠DNB的大小是否发生变化，若不变，求出∠DNB的度数，若变化，说明理由．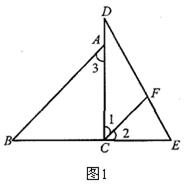
解方程组：
（1）
（2）