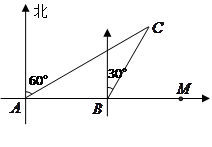【原创】去年我市教育局开展了认领“文明清单”活动,今年开学为落实认领“文明清单”活动,我校初一、初二两个年组对活动情况进行了统计,落实后的清单条数由落实前的清单条数与落实后认领的条数两部分组成(已知落实前每个年组的清单条数相同,落实后人均条数一样),下表是初一、初二的学生数及落实后清单条数的情况信息:
| |
初一 |
初二 |
初三 |
| 人数 |
200 |
180 |
210 |
| 清单总数(条) |
1800 |
1700 |
|
(1)试求落实前各年组的清单总数及落实后人均认领清单条数?
(2)如果初三年组想要清单条数达到2480条,那么初三年组人均应该认领多少条?
如图,直线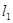 交直线
交直线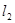 于
于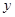 轴上一点
轴上一点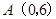 ,交
,交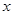 轴上另一点
轴上另一点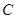 ,
,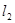 交
交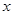 轴于另一点
轴于另一点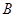 ,二次函数
,二次函数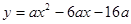 (
(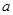 >0)的图像过点
>0)的图像过点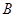 、
、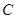 两点,点
两点,点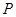 是线段
是线段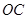 上由
上由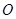 向
向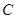 移动的动点,线段
移动的动点,线段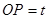 (1<
(1<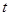 <8)。
<8)。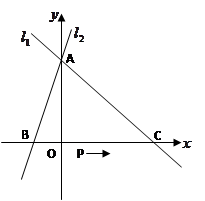
⑴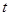 为何值时,
为何值时,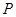 为圆心
为圆心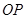 为半径的圆与
为半径的圆与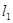 相切;
相切;
⑵设抛物线对称轴与直线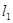 相交于点
相交于点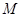 ,请在
,请在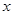 轴上求一点
轴上求一点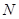 ,使
,使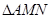 的周长最小;
的周长最小;
⑶设点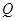 是
是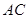 上由
上由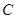 向
向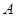 移动的一动点,且
移动的一动点,且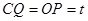 ,若
,若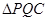 的面积为
的面积为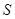 ,求
,求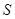 与
与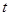 的函数关系式,当
的函数关系式,当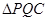 为等腰三角形时,请直接写出
为等腰三角形时,请直接写出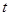 的值。
的值。
如图,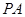 为⊙O的切线,
为⊙O的切线,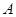 为切点,连接
为切点,连接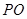 并延长,与圆相交于点
并延长,与圆相交于点 ,
,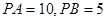 ,∠
,∠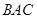 的平分线与
的平分线与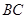 和⊙O分别相交于点
和⊙O分别相交于点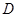 和
和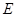 。
。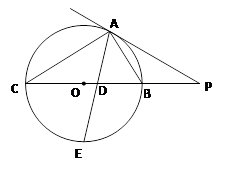
求:⑴⊙O的半径;⑵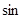 ∠
∠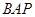 的值;⑶
的值;⑶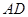 ·
· 的值。
的值。
已知,关于的 方程
方程 (
( 为整数)的根为整数,双曲线
为整数)的根为整数,双曲线
 >0
>0 过梯形
过梯形 的顶点
的顶点 和腰
和腰 中点
中点 ,如图所示,且∠
,如图所示,且∠ ,求四边形
,求四边形 的面积。
的面积。
如图, 是矩形纸片,翻折∠
是矩形纸片,翻折∠ 、∠
、∠ 使
使 边、
边、 边恰好落在
边恰好落在 上。设
上。设 分别是
分别是 落在AC上的两点,
落在AC上的两点, 分别是折痕
分别是折痕 与
与 的交点。
的交点。
⑴请根据题意,利用尺规作图作出点F、H及折痕CE、AG;
⑵顺次连接G、F、E、H,试确定四边形GFEH的形状,并说明理由。
如图,某货船以24海里/时的速度将一批重要物资从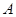 处运往正东方向的
处运往正东方向的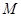 处,在点
处,在点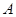 处测得某岛
处测得某岛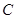 在北偏东
在北偏东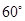 的方向上.该货船航行
的方向上.该货船航行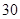 分钟后到达
分钟后到达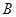 处,此时再测得该岛在北偏东
处,此时再测得该岛在北偏东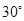 的方向上,已知在
的方向上,已知在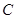 岛周围
岛周围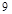 海里的区域内有暗礁.若继续向正东方向航行,该货船有无触礁危险?试说明理由.
海里的区域内有暗礁.若继续向正东方向航行,该货船有无触礁危险?试说明理由.