学完“证明（二）”一章后，老师布置了一道思考题：如图，点M、N分别在正三角形ABC的边BC．CA上，且BM=CN，AM、BN交于点Q。求证：∠BQM=60°。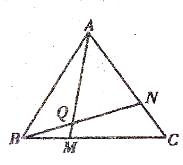
（1）请你完成这道思考题；
（2）做完（1）后，同学们在老师的启发下进行了反思，提出了许多问题，如：
①若将题中“BM=CN”与“∠BQM=60°”的位置交换，得到的是否仍是真命题?
②若将题中的点M，N分别移动到BC，CA的延长线上，是否仍能得到∠BQM＝60°？
③若将题中的条件“点M，N分别在正三角形ABC的BC、CA边上”改为“点M，N分别在正方形ABCD的BC，CD边上”，是否仍能得到∠BQM＝60°？对②，③进行证明。（自己画出对应的图形）
（11·
珠海）如图，在正方形ABC1D1中，AB＝1．连接AC1，
以AC1为边作第二个正方形AC1C2D2；连接AC2，以AC2为边作第三个正方形AC2C3D3．
（1）求第二个正方形AC1C2D2和第三个正方形的边长AC2C3D3；
（2）请直接写出按此规律所作的第7个正方形的边长．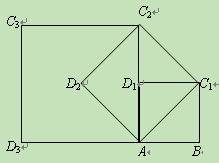
（11·珠海）八年级学生到距离学校15千米的农科所参观，一部分学生骑自行车先走，过了40分钟后，其余同学乘汽车出发，结果两者同时到达．若汽车的速度是骑自行车同学速度的3倍，求骑自行车同学的速度．
（11·珠海）如图，在Rt△ABC中，∠C＝90°．
（1）求作：△ABC的一条中位线，与AB交于D点，与BC交于E点．（保留作图痕迹，不
写作法）
（2）若AC＝6，AB＝10，连结CD，则DE＝_▲，CD＝_▲．
（11·珠海）某校为了调查学生视力变化情况，从该校2008年
入校的学生中抽取了部分学生进行连续三年的视力跟踪调查，将所得数据处理，制成拆线统
计图和扇形统计图，如图所示：
（1）该校被抽查的学生共有多少名？
（2）现规定视力5.1及以上为合格，若被抽查年级共有600名学生，估计该年级在2010年有多少名学生视力合格．
如图，在Rt△ABC中，∠C=90°，AC=8，BC=6，点P在AB上，AP=2，点E、F同时从点P出发，分别沿PA、PB以每秒1个单位长度的速度向点A、B匀速运动，点E到达点A后立刻以原速度沿AB向点B运动，点F运动到点B时停止，点E也随之停止．在点E、F运动过程中，以EF为边作正方形EFGH，使它与△ABC在线段AB的同侧．设E、F运动的时间为t/秒（t＞0），正方形EFGH与△ABC重叠部分面积为S．
（1）当时t=1时，正方形EFGH的边长是_______．当t=3时，正方形EFGH的边长是_______
（2）当0＜t≤2时，求S与t的函数关系式；
（3）直接答出：在整个运动过程中，当t为何值时，S最大？最大面积是多少？