某公司为了扩大经营,决定购买 台机器用于生产活塞.现有甲、乙两种机器供选择,其中每种机器的价格和每台机器的日产量如下表所示.经过预算,本次购买机器所需的资金不能超过 万元.

(1)按该公司的要求,可以有几种购买方案?
(2)若该公司购进的 台机器的日生产能力不能低于 个,为了节约资金,应选择哪种购买方案?
甲、乙两名同学进入初三后,某科6次考试成绩如图:(1)请根据下图填写如表:
| 平均数 |
方差 |
中位数 |
众数 |
极差 |
|
| 甲 |
75 |
75 |
|||
| 乙 |
33.3 |
15 |
(2)请你分别从以下两个不同的方面对甲、乙两名同学6次考试成绩进行分析:
①从平均数和方差相结合看;
②从折线图上两名同学分数的走势上看,你认为反映出什么问题?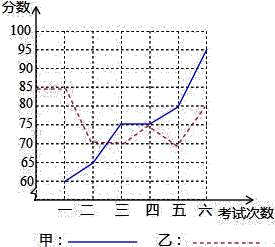
解方程组: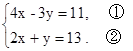
如图,在△ABC中,AB=AC,DE是边AB垂直平分线交AB于E,交AC于D,连结BD。
(1)若∠A=40°,求∠DBC的度数。
(2)若△BCD的周长为12cm,△ABC的周长为18cm,求BE的长。
△ABC是等边三角形,AB=8,AD是BC边上的高,DE⊥AC,求CE的长度.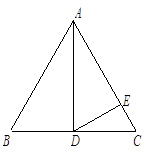
如图,已知AB=DE,AB∥DE,AF=DC。求证:BC∥EF。