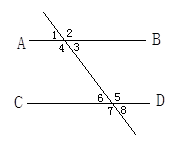计算: .
如图,已知AD⊥BC于D,EG⊥BC于G,∠E=∠3,AD平分∠BAC吗?若平分,请写出推理过程;若不平分,试说明理由.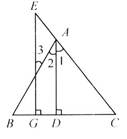
如图,已知直线m∥n,A、B为直线n上两点,C、D为直线m上两点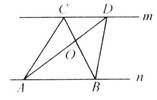
(1)请写出图中面积相等的三角形;
(2)如果A、B、C为三个定点,点D在m上移动,那么,无论D点移动到任何位置,总有___________与△ABC的面积相等,理由是:________________________.
阅读:如图,CE∥AB,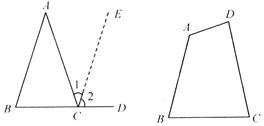
∴∠1=∠A,∠2=∠B.
∴∠ACD=∠1+∠2=∠A+∠B,这是一个有用的事实,请用这个事实,在如图5-102四边形ABCD内引一条和边平行的直线,求出∠A+∠B+∠C+∠D的度数.
已知:如图5-,AB∥CD,直线EF分别交AB、CD于点E、F,∠BEF的平分线与∠DEF的平分线相交于点P.求证∠P=90°.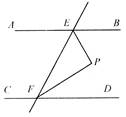
如图所示,请写出能够得到直线AB∥CD的所有直接条件.