如图,已知等边△ABC,AB=16,以AB为直径的半圆与BC边交于点D,过点D作DF⊥AC,垂足为F,过点F作FG⊥AB,垂足为G,连结GD.

(1)求证:DF是⊙O的切线;
(2)求FG的长;
(3)求tan∠FGD的值.
设p:函数 的定义域为R; q:不等式
的定义域为R; q:不等式 ,对
,对
 ∈(-∞,-1)上恒成立,如果命题“p∨q”为真命题,命题“p∧q”为假命题,求实数
∈(-∞,-1)上恒成立,如果命题“p∨q”为真命题,命题“p∧q”为假命题,求实数 的取值范围.
的取值范围.
已知 在区间
在区间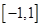 上是增函数.
上是增函数.
(1)求实数 的值组成的集合
的值组成的集合 ;
;
(2)设关于 的方程
的方程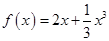 的两个非零实根为
的两个非零实根为 、
、 .试问:是否存在实数
.试问:是否存在实数 ,使得不等式
,使得不等式 对任意
对任意 及
及 恒成立?若存在,求
恒成立?若存在,求 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
已知椭圆 ,
, 、
、 是其左右焦点,离心率为
是其左右焦点,离心率为 ,且经过点
,且经过点 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)若 、
、 分别是椭圆长轴的左右端点,
分别是椭圆长轴的左右端点, 为椭圆上动点,设直线
为椭圆上动点,设直线
 斜率为
斜率为 ,且
,且 ,求直线
,求直线 斜率的取值范围;
斜率的取值范围;
(3)若 为椭圆上动点,求
为椭圆上动点,求 的最小值.
的最小值.
数列 的前
的前 项和记为
项和记为 ,
, ,
, .
.
(1)求数列 的通项公式;
的通项公式;
(2)等差数列 的前
的前 项和
项和 有最大值,且
有最大值,且 ,又
,又 、
、 、
、 成等比数列,求
成等比数列,求 .
.
如图,四棱锥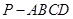 的底面是正方形,
的底面是正方形, 底面
底面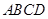 ,
,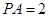 ,
, ,点
,点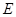 、
、 分别为棱
分别为棱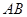 、
、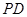 的中点.
的中点.
(1)求证: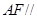 平面
平面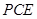 ;
;
(2)求证:平面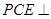 平面
平面 ;
;
(3)求三棱锥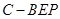 的体积.
的体积.