有这样一个问题:探究同一平面直角坐标系中系数互为倒数的正、反比例函数 与 的图象性质.
小明根据学习函数的经验,对函数 与 ,当 时的图象性质进行了探究.
下面是小明的探究过程:
(1)如图所示,设函数 与 图象的交点为 , ,已知 点的坐标为 ,则 点的坐标为 ;
(2)若点 为第一象限内双曲线上不同于点 的任意一点.
①设直线 交 轴于点 ,直线 交 轴于点 .求证: .
证明过程如下:设 ,直线 的解析式为 .
则 ,
解得
直线 的解析式为
请你把上面的解答过程补充完整,并完成剩余的证明.
②当 点坐标为 , 时,判断 的形状,并用 表示出 的面积.

如图,AB是⊙O的直径,C是AB延长线上一点,CD与⊙O相切于点E,AD⊥CD于点D.
(1)求证:AE平分∠DAC;
(2)若AB=4,∠ABE=60°.
①求AD的长;
②求出图中阴影部分的面积.
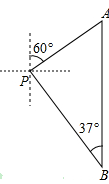
周末,小亮一家在瘦西湖游玩,妈妈在岸边 处观看小亮与爸爸在湖中划船(如图).小船从
处观看小亮与爸爸在湖中划船(如图).小船从 处出发,沿北偏东60°划行300米到达A处,接着向正南方向划行一段时间到达B处.在B处小亮观测妈妈所在的P处在北偏西37°方向上,这时小亮与妈妈相距多少米(精确到1米)?(参考数据:
处出发,沿北偏东60°划行300米到达A处,接着向正南方向划行一段时间到达B处.在B处小亮观测妈妈所在的P处在北偏西37°方向上,这时小亮与妈妈相距多少米(精确到1米)?(参考数据:
 ,
, )
)
阅读对话,解答问题.
(1)分别用 、
、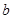 表示小冬从小丽、小兵袋子中抽出的卡片上标有的数字,请用树状图法或列表法写出(
表示小冬从小丽、小兵袋子中抽出的卡片上标有的数字,请用树状图法或列表法写出( ,
,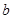 ) 的所有取值;
) 的所有取值;
(2)求点( ,
,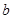 )在一次函数
)在一次函数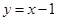 图像上的概率.
图像上的概率.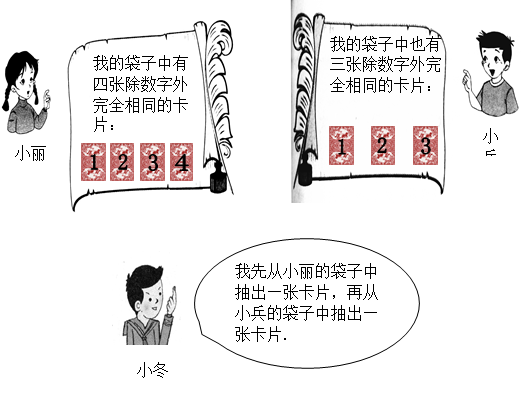
如图,已知△ABC,按如下步骤作图:①分别以A、C为圆心,以大于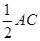 的长为半径在AC两边作弧,交于两点M、N;②作直线MN,分别交AB、AC于点D、O;③过C作CE∥AB交MN于点E,连接AE、CD.
的长为半径在AC两边作弧,交于两点M、N;②作直线MN,分别交AB、AC于点D、O;③过C作CE∥AB交MN于点E,连接AE、CD.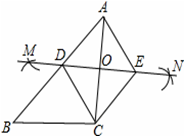
(1)求证:四边形ADCE是菱形;
(2)当∠ACB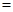 90°,BC
90°,BC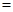 6,AB
6,AB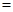 10,求四边形ADCE的面积.
10,求四边形ADCE的面积.
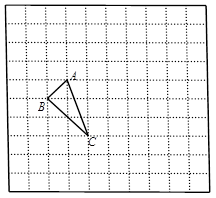
如图,正方形网格中每个小正方形边长都是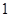 ,每个小格的顶点叫格点,以格点为顶点的三角形叫做格点三角形.①求格点△
,每个小格的顶点叫格点,以格点为顶点的三角形叫做格点三角形.①求格点△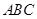 的面积;②在网格图中画出△
的面积;②在网格图中画出△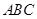 先向右平移
先向右平移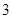 个单位,再向上平移
个单位,再向上平移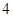 个单位后的△
个单位后的△ ;③画出格点△
;③画出格点△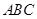 绕点
绕点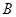 顺时针旋转90°后的△
顺时针旋转90°后的△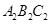 .
.