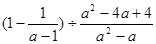(1)操作发现:如图①,小明画了一个等腰三角形 ,其中 ,在 的外侧分别以 , 为腰作了两个等腰直角三角形 , ,分别取 , , 的中点 , , ,连接 , .小明发现了:线段 与 的数量关系是 ;位置关系是 .
(2)类比思考:
如图②,小明在此基础上进行了深入思考.把等腰三角形 换为一般的锐角三角形,其中 ,其它条件不变,小明发现的上述结论还成立吗?请说明理由.
(3)深入研究:
如图③,小明在(2)的基础上,又作了进一步的探究.向 的内侧分别作等腰直角三角形 , ,其它条件不变,试判断 的形状,并给与证明.

对某校九 年级随机抽取若干名学生进行体能测试,成绩按A、B、C、D四个等级进行了评定.现将抽取学生的成绩评定结果进行分析,并绘制扇形统计图和条形统计图如下: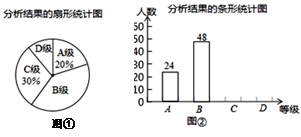
根据上述信息完成下列问题:
(1)这次抽取的样本的容量为;图①中“D级”对应的扇形圆心角度数为°
(2)请在图②中把条形统计图补充完整;
(3)已知该校九年级共有学生750名,请你估计体能达到A级和B级的共约有多少人.
盒子中有4个球,每个球上写有1~4中的一个数字,不同的球上数字不同.
(1)若从盒中取三个球,以球上所标数字为线段的长,则能构成三角形的概率是多少?
(2)若小明从盒中取出一个球,放回后再取出一个球,然后让小华猜两球上的数字之和,你认为小华猜和为多少时 ,猜中的可能性大.请说明理由.
如图,已知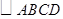 中,F是BC边的中点,连接DF并延长,交AB的延长线于点E.求证:AB=BE.
中,F是BC边的中点,连接DF并延长,交AB的延长线于点E.求证:AB=BE.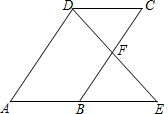
(1)解不等式组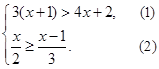 (2)解方程:
(2)解方程: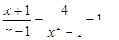
(1)计算: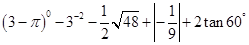 (2)
(2)