(本题6分)
（1）计算： 4cos²45°-|-2| + tan45°；
（2）分解因式：

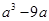
同学们，我们曾经研究过n×n的正方形网格，得到了网格中正方形的总数的表达式为1²+2²+3²+…+n²．但n为100时，应如何计算正方形的具体个数呢?下面我们就一起来探究并解决这个问题．首先，通过探究我们已经知道0×1+1×2+2×3+…+(n—1)×n=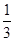n(n+1)(n—1)时，我们可以这样做：
(1)观察并猜想：
1²+2²=(1+0)×1+(1+1)×2=1+0×1+2+1×2=(1+2)+(0×1+1×2)
1²+2²+3²=(1+0)×1+(1+1)×2+(1+2)×3
=1+0×1+2+1×2+3+2×3
=(1+2+3)+(0×1+1×2+2×3)
1²+2²+3²+4²=(1+0)×1+(1+1)×2+(1+2)×3+
=1+0×1+2+1×2+3+2×3+
=(1+2+3+4)+()
……
(2)归纳结论：
1²+2²+3²+…+n²=(1+0)×1+(1+1)×2+(1+2)×3+…+n
=1+0×1+2+1×2+3+2×3+…+n+(n一1)×n
=() +
=+
=×
(3)实践应用：
通过以上探究过程，我们就可以算出当n为100时，正方形网格中正方形的总个数是．

观察下面的变形规律：
＝1－； ＝－；＝－；……
解答下面的问题：
（1）若n为正整数，请你猜想＝ ；
（2）证明你猜想的结论；
（3）求和：＋＋＋…＋.

如图，⊙Ｏ是Rt△ABC的内切圆，∠ACB＝90°，AB＝13，AC＝12，
求图中阴影部分的面积

体育测试时，初三一名高个学生推铅球，已知铅球所经过的路线为抛物线的一部分，根据关系式回答：

该同学的出手最大高度是多少？
铅球在运行过程中离地面的最大高度是多少？
该同学的成绩是多少？