同学们，我们曾经研究过n×n的正方形网格，得到了网格中正方形-优题课

同学们，我们曾经研究过n×n的正方形网格，得到了网格中正方形的总数的表达式为1²+2²+3²+…+n²．但n为100时，应如何计算正方形的具体个数呢?下面我们就一起来探究并解决这个问题．首先，通过探究我们已经知道0×1+1×2+2×3+…+(n—1)×n=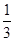n(n+1)(n—1)时，我们可以这样做：
(1)观察并猜想：
1²+2²=(1+0)×1+(1+1)×2=1+0×1+2+1×2=(1+2)+(0×1+1×2)
1²+2²+3²=(1+0)×1+(1+1)×2+(1+2)×3
=1+0×1+2+1×2+3+2×3
=(1+2+3)+(0×1+1×2+2×3)
1²+2²+3²+4²=(1+0)×1+(1+1)×2+(1+2)×3+
=1+0×1+2+1×2+3+2×3+
=(1+2+3+4)+(                                  )
……
(2)归纳结论：
1²+2²+3²+…+n²=(1+0)×1+(1+1)×2+(1+2)×3+…+n
=1+0×1+2+1×2+3+2×3+…+n+(n一1)×n
=(                      ) +
=                      +
=×
(3)实践应用：
通过以上探究过程，我们就可以算出当n为100时，正方形网格中正方形的总个数是              ．

科目数学题型解答题难度中等

知识点：幂的乘方与积的乘方

在 $⊙ O$ 中， $AB$ 为直径， $C$ 为 $⊙ O$ 上一点．

（Ⅰ）如图1．过点 $C$ 作 $⊙ O$ 的切线，与 $AB$ 的延长线相交于点 $P$ ，若 $∠ CAB = 27 °$ ，求 $∠ P$ 的大小；

（Ⅱ）如图2， $D$ 为 $\hat{AC}$ 上一点，且 $OD$ 经过 $AC$ 的中点 $E$ ，连接 $DC$ 并延长，与 $AB$ 的延长线相交于点 $P$ ，若 $∠ CAB = 10 °$ ，求 $∠ P$ 的大小．

在一次中学生田径运动会上，根据参加男子跳高初赛的运动员的成绩（单位： $m)$ ，绘制出如下的统计图①和图②，请根据相关信息，解答下列问题：

（Ⅰ）图1中 $a$ 的值为　　；

（Ⅱ）求统计的这组初赛成绩数据的平均数、众数和中位数；

（Ⅲ）根据这组初赛成绩，由高到低确定9人进入复赛，请直接写出初赛成绩为 $1.65 m$ 的运动员能否进入复赛．

解不等式 $\{\begin{matrix} x + 2 ⩽ 6, ① \\ 3 x - 2 ⩾ 2 x, ② \end{matrix}$ ，请结合题意填空，完成本题的解答．

（Ⅰ）解不等式①，得　　；

（Ⅱ）解不等式②，得　　；

（Ⅲ）把不等式①和②的解集在数轴上表示出来；

（Ⅳ）原不等式组的解集为　　．

综合与探究

如图，抛物线 $y = a x^{2} + bx + 6$ 经过点 $A (- 2, 0)$ ， $B (4, 0)$ 两点，与 $y$ 轴交于点 $C$ ，点 $D$ 是抛物线上一个动点，设点 $D$ 的横坐标为 $m (1 < m < 4)$ ．连接 $AC$ ， $BC$ ， $DB$ ， $DC$ ．

（1）求抛物线的函数表达式；

（2） $ΔBCD$ 的面积等于 $ΔAOC$ 的面积的 $\frac{3}{4}$ 时，求 $m$ 的值；

（3）在（2）的条件下，若点 $M$ 是 $x$ 轴上一动点，点 $N$ 是抛物线上一动点，试判断是否存在这样的点 $M$ ，使得以点 $B$ ， $D$ ， $M$ ， $N$ 为顶点的四边形是平行四边形？若存在，请直接写出点 $M$ 的坐标；若不存在，请说明理由．

综合与实践

动手操作：

第一步：如图1，正方形纸片 $ABCD$ 沿对角线 $AC$ 所在的直线折叠，展开铺平．在沿过点 $C$ 的直线折叠，使点 $B$ ，点 $D$ 都落在对角线 $AC$ 上．此时，点 $B$ 与点 $D$ 重合，记为点 $N$ ，且点 $E$ ，点 $N$ ，点 $F$ 三点在同一条直线上，折痕分别为 $CE$ ， $CF$ ．如图2．

第二步：再沿 $AC$ 所在的直线折叠， $ΔACE$ 与 $ΔACF$ 重合，得到图3．

第三步：在图3的基础上继续折叠，使点 $C$ 与点 $F$ 重合，如图4，展开铺平，连接 $EF$ ， $FG$ ， $GM$ ， $ME$ ．如图5，图中的虚线为折痕．

问题解决：

（1）在图5中， $∠ BEC$ 的度数是　　， $\frac{AE}{BE}$ 的值是　　．

（2）在图5中，请判断四边形 $EMGF$ 的形状，并说明理由；

（3）在不增加字母的条件下，请你以图中5中的字母表示的点为顶点，动手画出一个菱形（正方形除外），并写出这个菱形：　　．