(本题13分)在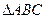 中,内角
中,内角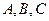 的对边分别为
的对边分别为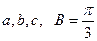 ,
,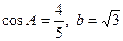 。(1)求边
。(1)求边 的大小;(2)求
的大小;(2)求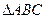 的面积。
的面积。

为了了解《中华人民共和国道路交通安全法》在学生中的普及情况,调查部门对某校6名学生进行问卷调查,6人得分情况如下:
5 6 7 8 9 10
把这6名学生的得分看成一个总体.
(Ⅰ)求该总体的平均数;
(Ⅱ)用简单随机抽样的方法从6名学生中抽取2名,他们的得分组成一个样本.求该样本平均数与总体平均数之差的绝对值不超过0.5的概率
已知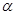 是三角形的内角,且
是三角形的内角,且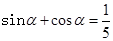
(Ⅰ)求 的值;
的值;
(Ⅱ)把 用
用 表示出来,并求其值
表示出来,并求其值
为了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如上图),图中从左到右各小长方形面积之比为2: 4: 17: 15: 9: 3,第二小组的频数为12.
(Ⅰ)第二小组的频率是多少?样本容量是多少?
(Ⅱ)若次数在110以上(含110次)为达标,试估计学校全体高一学生的达标率是多少?
为了对某课题进行研究,用分层抽样方法从三所高校A,B,C的相关人员中,抽取若干人组成研究小组,有关数据如下表(单位:人).
(Ⅰ)求x,y;
(Ⅱ)若从高校B,C抽取的人中选2人作专题发言,求这2人都来自高校C概率.
| 高校 |
相关人数 |
抽取人数 |
| A |
18 |
x |
| B |
36 |
2 |
| C |
54 |
y |
化简: (其中
(其中 为第三象限角).
为第三象限角).